Análisis dimensional

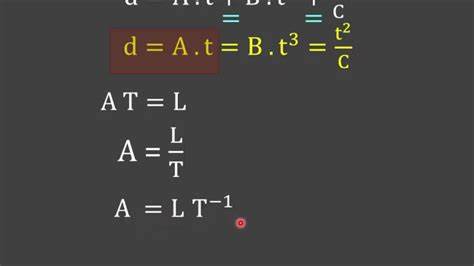
Su resultado fundamental, el teorema π de Vaschy-Buckingham (más conocido por teorema π) permite cambiar el conjunto original de parámetros de entrada dimensionales de un problema físico por otro conjunto de parámetros de entrada adimensionales más reducido. Estos parámetros adimensionales se obtienen mediante combinaciones adecuadas de los parámetros dimensionales y no son únicos, aunque sí lo es el número mínimo necesario para estudiar cada sistema. De este modo, al obtener uno de estos conjuntos de tamaño mínimo se consigue:

El análisis dimensional es la base de los ensayos con maquetas a escala reducida utilizados en muchas ramas de la ingeniería, tales como la aeronáutica, la automoción o la ingeniería civil. A partir de dichos ensayos se obtiene información sobre lo que ocurre en el fenómeno a escala real cuando existe semejanza física entre el fenómeno real y el ensayo, gracias a que los resultados obtenidos en una maqueta a escala son válidos para el modelo a tamaño real si los números adimensionales que se toman como variables independientes para la experimentación tienen el mismo valor en la maqueta y en el modelo real. Así, para este tipo de cálculos, se utilizan ecuaciones dimensionales, que son expresiones algebraicas que tienen como variables a las unidades fundamentales y derivadas, las cuales se usan para demostrar fórmulas, equivalencias o para dar unidades a una respuesta.

Finalmente, el análisis dimensional también es una herramienta útil para detectar errores en los cálculos científicos e ingenieriles. Con este fin se comprueba la congruencia de las unidades empleadas en los cálculos, prestando especial atención a las unidades de los resultados.

Para reducir un problema dimensional a otro adimensional con menos parámetros (porque las variables de trabajo se reducen a números adimensionales), se siguen los siguientes pasos generales:

Calculemos mediante Análisis Dimensional la velocidad de un cuerpo en caída libre. Sabemos que dicha velocidad ${displaystyle v}$ dependerá de la altura ${displaystyle h}$ y de la gravedad ${displaystyle g}$. Pero imaginemos que también se nos ocurre decir que la velocidad depende de la masa ${displaystyle m}$. Una de las bondades del Análisis Dimensional es que es "autocorregible", es decir, el procedimiento, por sí solo, elimina las unidades que no son necesarias.

${displaystyle [v]={ ext{m/s}}={ ext{LT}}^{-1},quad [g]={ ext{m/s}}^{2}={ ext{LT}}^{-2},quad [h]={ ext{m}}={ ext{L}},quad [m]={ ext{kg}}={ ext{M}}}$

Aquí tenemos que decir que ${displaystyle displaystyle epsilon _{k}}$ se refiere al exponente de la unidad ${displaystyle displaystyle k}$, pero eso se verá en pasos sucesivos.

Se forma un sistema de ecuaciones. Si nos fijamos, tenemos 4 incógnitas, y sólo 3 ecuaciones, así que para que el sistema pueda ser resuelto, necesitamos tantas incógnitas como ecuaciones. ¿Cómo se subsana el problema? Muy sencillo: se coge un ${displaystyle displaystyle epsilon _{k}}$ cualquiera y le asignamos el valor que queramos, a excepción del 0. En nuestro caso, vamos a tomar ${displaystyle displaystyle epsilon _{v}}$ como ${displaystyle displaystyle 1}$.

Si aplicamos la solución inicial que hemos propuesto anteriormente (${displaystyle displaystyle epsilon _{v}=1}$), se realizan los sencillos cálculos y llegamos a las soluciones:

Un grupo ${displaystyle displaystyle Pi }$ es una ecuación adimensional. ¿Cuántos grupos ${displaystyle displaystyle Pi }$ vamos a obtener? Pues si ${displaystyle displaystyle m}$ es el número de unidades (las unidades son el metro, el kilo, el segundo, el grado, ...), y ${displaystyle displaystyle h}$ el rango máximo de la matriz que contiene los coeficientes de las magnitudes de las unidades (a veces coincide el rango de la matriz con el número de variables que tenemos, aunque ésta no es una regla fiable), el número de grupos ${displaystyle displaystyle Pi }$ (o ecuaciones que obtendremos) será ${displaystyle displaystyle m-h}$. En el caso que nos ocupa, ${displaystyle displaystyle 4-3=1}$ ecuación.

Ahora se cogen las unidades que hemos tomado en nuestro problema y las elevamos a los exponentes que hemos obtenido. Esa es nuestra ecuación.

(Nótese que ${displaystyle displaystyle Pi }$ es adimensional). Aquí obtenemos aquello que llamábamos "autocorrección": el exponente de la masa es 0, así que desaparece de nuestra ecuación, demostrando una vez más que la caída libre no depende de la masa del objeto en cuestión.

con ${displaystyle displaystyle k}$ valiendo ${displaystyle displaystyle {sqrt {2}}}$, lo que nos da la fórmula correcta:

El principio de Fourier homogeneidad dimensional es un principio de buena formación de las expresiones que relacionan magnitudes físicas de manera algebraica. Es decir, es un principio de consistencia matemática que postula solo es posible sumar o restar entre sí magnitudes físicas de la misma naturaleza. En consecuencia, no podemos sumar longitud con tiempo, o masa con longitud, etc.

El principio puede ilustrarse, con el ejemplo, de la energía de un cuerpo que es la suma de su energía cinética más su energía potencial:

Expresando la energía cinética y potencial tendremos:

Expresando la velocidad y la aceleración según las magnitudes fundamentales:

Expresado en forma dimensional:

Como puede verse tanto la energía cinética: un medio de la masa por la velocidad al cuadrado y la energía potencial: la masa por la gravedad y por la altura, es en ambos casos energía con la misma ecuación dimensional.

Por tanto, este principio de Fourier garantiza la coherencia de una ecuación física. Es importante recordar que si bien las constantes numéricas son adimensionales (ecuación dimensional igual a la unidad), por otro lado las constantes físicas tienen dimensión diferente de la unidad: