Competencia de Cournot

¿Qué día cumple años Competencia de Cournot?

Competencia de Cournot cumple los años el 18 de enero.

---

¿Qué día nació Competencia de Cournot?

Competencia de Cournot nació el día 18 de enero de 877.

---

¿Cuántos años tiene Competencia de Cournot?

La edad actual es 1146 años. Competencia de Cournot cumplirá 1147 años el 18 de enero de este año.

---

¿De qué signo es Competencia de Cournot?

Competencia de Cournot es del signo de Capricornio.

---

El modelo de competencia de Cournot es un modelo económico usado para describir una estructura de industrias en la que las compañías compiten en las cantidades que van a producir. Lo deciden independientemente de la otra industria y toman la decisión al mismo tiempo. Debe su nombre a Antoine Augustin Cournot (1801-1877) que se inspiró al observar la competencia en duopolio el mercado de agua mineral embotellada. Tiene las siguientes características:

Un supuesto esencial de este modelo son las variaciones conjeturales nulas, de este modo, cada firma tiene como objetivo la maximización de sus beneficios, basándose en la expectativa de que su propia decisición no tendrá un efecto en las decisiones de sus rivales, El precio es una función decreciente de la oferta total. Todas las firmas conocen que existen ${displaystyle N}$ firmas en el mercado, y toman la producción de las demás como dadas. Cada firma tiene una función de costos ${displaystyle c_{i}(q_{i})}$. Normalmente las funciones de costos son tratadas como conocimiento general(todas las firmas conocen las funciones de costos de las demás firmas). Las funciones de costos pueden ser iguales o diferentes entre las firmas. El precio del mercado es tal que la demanda es igual a la cantidad producida por todas las firmas. Cada firma toma la cantidad a producir de sus competidores como dada, evalúa la demanda residual y se comporta como un monopolio.

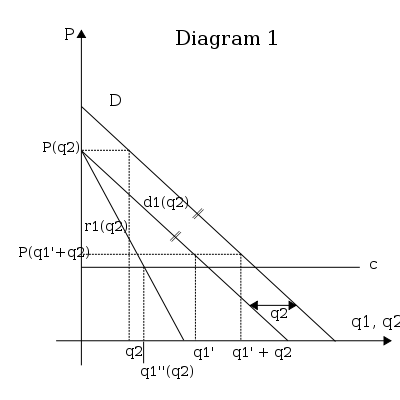
Esta sección presenta un análisis del modelo con 2 agentes y costos marginales constantes.

Los precios de Equilibrio serán:

Esto implica que el beneficio del agente 1 está dado por ${displaystyle Pi _{1}=q_{1}(P(q_{1}+q_{2})-c)}$

Este es el punto donde los costos marginales interceptan los beneficios marginales correspondientes a ${displaystyle d_{1}(q^{c})}$.

En términos muy generales, sea la función de precios para una industria (duopolio) ${displaystyle P(q_{1}+q_{2})}$ y la firma ${displaystyle i}$ tiene la función de costos ${displaystyle C_{i}(q_{i})}$. Para calcular el equilibrio de Nash, las funciones de reacción deben calcularse primero.

El beneficio de la firma ${displaystyle i}$ es el beneficio menos los costos. El beneficio es el producto del precio por las cantidades y el costo es dado por la función de costos de la firma, así que las ganancias (como se describieron arriba) son: ${displaystyle Pi _{i}=P(q_{1}+q_{2}).q_{i}-C_{i}(q_{i})}$. La mejor respuesta es encontrar el valor de ${displaystyle q_{i}}$ que maximize ${displaystyle Pi _{i}}$ dado ${displaystyle q_{j}}$, con ${displaystyle i eq j}$, i.e. se encuentra la producción que maximiza el beneficio, dado una producción de la firma del otro duopolista. Entonces, se debe buscar el máximo valor de ${displaystyle Pi _{i}}$ con respecto a ${displaystyle q_{i}}$. Primero se toma la derivada de ${displaystyle Pi _{i}}$ con respecto a${displaystyle q_{i}}$:

Se iguala a cero para encontrar un máximo

Los valores de ${displaystyle q_{i}}$ que satisfacen esta ecuación son las mejores respuestas. Los equilibrios de Nash son donde ambos ${displaystyle q_{1}}$ y ${displaystyle q_{2}}$ son las mejores respuestas dados los valores de ${displaystyle q_{1}}$ y ${displaystyle q_{2}}$.

Suponga que la industria tiene la siguiente función de precios: ${displaystyle P(q_{1}+q_{2})=a-(q_{1}+q_{2})}$.

El beneficio de la firma ${displaystyle i}$ (con la función de costos ${displaystyle C_{i}(q_{i})}$ tal que ${displaystyle {frac {partial ^{2}C_{i}(q_{i})}{partial q_{i}^{2}}}=0}$ y ${displaystyle {frac {partial C_{i}(q_{i})}{partial q_{j}}}=0,j eq i}$ por facilidad de cálculo) es:

La maximización del problema genera (desde el caso general):

Sin perder la generalidad, considere el problema de la firma 1:

Por simetría:

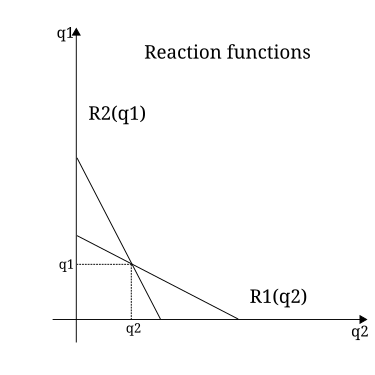
Estas son las funciones de reacción de las firmas. Para cualquier valor de ${displaystyle q_{2}}$, la firma 1 responde de la mejor manera posible con un ${displaystyle q_{1}}$ que satisface las funciones de arriba. En el equilibrio de Nash, ambas firmas estarán usando funciones de reacción para resolver simultáneamente las funciones de arriba.

Sustituyendo para ${displaystyle q_{2}}$ en la función de reacción de la firma 1:

El equilibrio de Nash simétrico está en ${displaystyle (q_{1}*,q_{2}*)}$. (Véase Holt (2005, Capítulo 13) para ejemplos asimétricos). Haciendo suposiciones apropiadas para las derivadas parciales (por ejemplo, asumir que los costos de cada firma es una función lineal con respecto a la cantidad y usando la pendiente de esa función en el cálculo), las cantidades de equilibrio pueden ser sustituidas en la función de precios de la industria${displaystyle P(q_{1}+q_{2})=a-(q_{1}+q_{2})}$ para obtener el precio de equilibrio del mercado.

Para un número arbitrario de agentes, N>1, las cantidades y el precio se pueden derivar de una manera análoga a la expuesta en la sección anterior. Con demandas lineales e idénticas y costos marginales constantes, los valores de equilibrio son los siguientes:

Demanda del Mercado; ${displaystyle p(q)=a-bq=a-bQ=p(Q)}$

Funciones de Costos; ${displaystyle c_{i}(q_{i})=cq_{i}}$, para todo i

${displaystyle q_{i}=Q/N={frac {a-c}{b(N+1)}}}$, producción individual de cada agente

${displaystyle sum q_{i}=Nq={frac {N(a-c)}{b(N+1)}}}$, producción total de la industria

${displaystyle p=a-b(Nq)={frac {a+Nc}{N+1}}}$, precio al que se vacía el mercado

y

${displaystyle Pi _{i}=left({frac {a-c}{N+1}} ight)^{2}left({frac {1}{b}} ight)}$, beneficio individual de cada agente

El teorema de Cournot dice que, en la ausencia de costos fijos de producción, cuando el número de agentes en el mercado, N, tiende al infinito, la producción del mercado, Nq, tiende a niveles de competencia perfecta y el precio converge a los costos marginales.

${displaystyle lim _{N ightarrow infty }p=c}$

Por eso con muchos agentes, un mercado de Cournot se aproxima a un mercado de competencia perfecta. Este resultado puede ser generalizado para el caso de agentes con distintas estructuras de costos (bajo ciertas restricciones) y demandas no lineales.

Cuando el mercado se caracteriza por tener costos fijos de producción, podemos endogeneizar el número de competidores imaginando que los agentes seguirán entrando en el mercado hasta que sus beneficios sean normales (es decir, no existan beneficios extraordinarios). En nuestro ejemplo lineal con ${displaystyle N}$ agentes, cuando existen costos fijos para cada agente y estos son ${displaystyle F}$, tenemos un número endógeno de agentes:

y una producción para cada agente que será igual a:

Este equilibrio es típicamente conocido como Equilibrio de Cournot con entradas endógenas, o Equilibrio de Marshall.^[1]​

Aunque ambos modelos tienen suposiciones similares, tienen implicaciones muy distintas:

Sin embargo, cuando el número de firmas tiende a infinito, el modelo de Cournot genera el mismo resultado que el modelo de Bertrand: el precio del mercado es el mismo que los costos marginales.

---