Perspectiva curvilínea

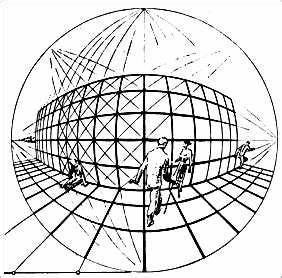
La perspectiva curvilínea es una proyección gráfica utilizada para dibujar objetos tridimensionales en superficies bidimensionales. Fue formalmente definida en 1968 por los artistas e historiadores del arte André Barre y Albert Flocon, en el libro "La Perspective curviligne".^[1]​ ^[2]​

Como antecedentes, se pueden citar las imágenes (poco precisas desde el punto de vista matemático), elaboradas por el miniaturista Jean Fouquet (1420-1481). Por su parte, se sabe que Leonardo da Vinci (1452-1519) trató sobre las perspectivas de líneas curvas en un cuaderno perdido.^[2]​

También se pueden encontrar ejemplos de una aproximación a una perspectiva de cinco puntos en el autorretrato del pintor manierista Parmigianino (1503-1540), en el que representó su propia imagen vista mediante un espejo curvo. Otro ejemplo sería el espejo curvo que aparece en el centro del Retrato del matrimonio Arnolfini (1434), obra del pintor Jan van Eyck (1390-1441).

El libro "Vanishing Point: Perspective for Comics from the Ground Up" (Punto de fuga: Perspectiva para los cómics desde cero), de Jason Cheeseman-Meyer,^[3]​ explica cómo realizar perspectivas con cuatro y cinco puntos de fuga.

En 1959, Albert Flocon había adquirido una copia de Grafiek en tekeningen, una obra de M. C. Escher que lo impresionó fuertemente por su uso de la perspectiva curvilínea y plegada, lo que influyó en la teoría que Flocon y Barre estaban desarrollando. Comenzaron una larga correspondencia, en la que Escher llamó a Flocon un "espíritu afín".^[2]​

Cuando se dibuja manualmente una perspectiva curvilínea, el sistema consiste en utilizar una rejilla de líneas de perspectiva curvas en lugar de usar las líneas rectas propias de la perspectiva cónica, lo que permite aproximar el dibujo a la imagen formada en la retina del ojo (que es esférica) con mayor precisión que en la perspectiva tradicional, que utiliza líneas rectas y adopta configuraciones extrañamente distorsionadas en los bordes del dibujo.

Se pueden utilizar cuatro, cinco, seis o más puntos de fuga:^[4]​

Las distancias a y c entre el observador y la pared son mayores que la distancia 'b, por lo que se adopta el principio de que cuando un objeto está a una distancia mayor del observador, se vuelve más pequeño. En consecuencia, la pared se reduce y, por lo tanto, aparece distorsionada en los bordes.

A continuación se describen las operaciones necesarias para obtener la imagen proyectada sobre un plano (el dibujo) de la proyección de un punto sobre una esfera desde su centro, en el que se sitúa el punto de vista:

Si un punto tiene las coordenadas cartesianas tridimensionales (x, y, z), entonces:

Denotando la distancia desde el punto al origen por

entonces la transformación del punto a un sistema de referencia curvilíneo de radio R es:

(si d = 0, entonces el punto está en el origen, lo que significa que su proyección no está definida)

Esto se deduce al proyectar primero el punto sobre una esfera de radio R centrada en el origen de coordenadas, de modo que se obtiene una imagen del punto que tiene las coordenadas

y a continuación se efectúa una segunda proyección, paralela al eje z, para representar a su vez la proyección del punto en la esfera ya calculado, sobre el plano del dibujo situado en z = R, obteniendo así

Como el dibujo descansa sobre el plano z = R, se ignoran las coordenadas z del punto de la imagen, obteniéndose así

Como modificar el radio de la esfera ${displaystyle R}$ equivale a una simple relación de escalado, generalmente se define como la unidad, lo que simplifica aún más la fórmula:

Una línea que no pasa por el origen se proyecta sobre un círculo máximo de la esfera, que se proyecta como una elipse sobre el plano del dibujo. La elipse tiene la propiedad de que su eje mayor es un diámetro del "círculo delimitador".

---