Ángulo


En geometría, el ángulo puede ser definido como la parte del plano determinada por dos semirrectas llamadas lados que tienen el mismo punto de origen llamado vértice del ángulo.
La medida de un ángulo es considerada como la amplitud del arco de circunferencia centrada en el vértice y delimitada por sus lados. Su medida es un múltiplo de la razón entre la longitud del arco y el radio. Su unidad natural es el radián, pero también se puede utilizar el grado sexagesimal o el grado centesimal.
Pueden estar definidos sobre superficies planas (trigonometría plana) o curvas (trigonometría esférica). Se denomina ángulo diedro al espacio comprendido entre dos semiplanos cuyo origen común es una recta. Un ángulo sólido es el que abarca un objeto visto desde un punto dado, midiendo su tamaño aparente.
Existen básicamente dos formas de definir un ángulo en el plano:
Euclides define un ángulo como la inclinación entre dos líneas que se encuentran una a otra en un plano y no están en línea recta. Según Proclo, un ángulo debe ser una calidad o una cantidad, o una relación. El primer concepto fue utilizado por Eudemo de Rodas, que describió un ángulo como desviación de una línea recta; el segundo por Carpo de Antioquía, que lo vio como el intervalo o el espacio entre las líneas que se intersecaban; Euclides adoptó un tercer concepto, aunque sus definiciones de ángulos rectos, agudos, y obtusos son cuantitativas.

Se denomina región angular a cada una de las dos partes en que queda dividido el plano por un ángulo.
Se llama amplitud de un ángulo a la medida de este.
Las unidades utilizadas para la medida de los ángulos del plano son:
Los ángulos se pueden medir mediante utensilios tales como el goniómetro, el cuadrante, el sextante, la ballestina, el transportador de ángulos o semicírculo graduado, graduador, etc.
Los ángulos, de acuerdo con su amplitud, reciben estas denominaciones:

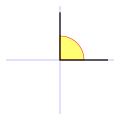
Es decir, mayor de 0° y menor de 90° (grados sexagesimales), o menor de 100g (grados centesimales).
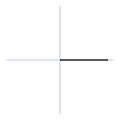
Es equivalente a 90° sexagesimales (o 100g centesimales).
Los dos lados de un ángulo recto son perpendiculares entre sí.
La proyección ortogonal de uno sobre otro es un punto, que coincide con el vértice.

Mayor a 90° y menor a 180° sexagesimales (o más de 100g y menos de 200g centesimales).
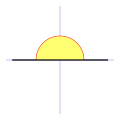
Equivalente a 180° sexagesimales (o 200g centesimales).
Los ángulos agudos y obtusos son ángulos oblicuos.

Equivalente a 360° sexagesimales (o 400g centesimales).
Se llama así a los ángulos que tienen el mismo lado final. Pueden ser en rotación contraria al ángulo dado o con una rotación mayor de 360°.
En un plano, dos semirrectas (no coincidentes ni alineadas) con un origen común determinan siempre dos ángulos, uno convexo (el de menor amplitud) y otro cóncavo (el de mayor amplitud):
Equivale a más de 0° y menos de 180°sexagesimales (o más de 0g y menos de 200g centesimales).

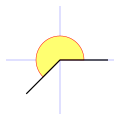
Esto es, más de 180° y menos de 360° sexagesimales (o más de 200g y menos de 400g centesimales).
Denominación relativo a su posición:
Denominación en función de la suma de su amplitud:
Cuando dos rectas son cortadas por una tercera, se forman las siguientes relaciones distantes:
Son los obtenidos mediante la suma o diferencia de ángulos. En la figura se representan dos sectores circulares contiguos, cada uno con su ángulo, denominados α y β respectivamente; la unión de los dos sectores tendrá por ángulo la composición, en este caso la suma, α + β, de los ángulos de los sectores que unimos.
Las razones trigonométricas de los ángulos compuestos están relacionadas con la de los ángulos componentes mediante las fórmulas de razones trigonométricas de ángulos compuestos, ver por ejemplo Identidades trigonométricas.

En función de su posición, se denominan:
Un ángulo, respecto de una circunferencia, pueden ser:
Ángulo central, si tiene su vértice en el centro de esta.
Ángulo inscrito, si su vértice es un punto de la circunferencia y sus lados la cortan en dos puntos.
Ángulo semi-inscrito, si su vértice está sobre esta, uno de sus lados la corta y el otro es tangente, siendo el punto de tangencia el propio vértice.
Ángulo interior, si su vértice está en el interior de la circunferencia.

Ángulo exterior, si tiene su vértice en el exterior de esta.
La trisección del ángulo es un problema clásico que consiste en dividir un ángulo dado en tres partes iguales usando solo regla y compás. En general, es imposible de resolver con esas condiciones.
Dado un espacio vectorial, cuyo cuerpo es el conjunto de los números reales y en el que existe un producto escalar entre vectores , se define el ángulo formado por dos vectores no nulos e mediante la expresión:
Si el cociente anterior es 0, se dice que ambos vectores son ortogonales o perpendiculares. El cociente anterior está en el intervalo debido a la desigualdad de Cauchy-Schwarz, lo que garantiza que siempre puede aplicarse el arcocoseno. Normalmente, se toma la rama del arcocoseno de forma que el ángulo que forman dos vectores siempre está en el intervalo (geométricamente, se elige el menor de los ángulos que forman dos vectores). Las principales propiedades que cumple el ángulo de dos vectores son las siguientes:
Escribe un comentario o lo que quieras sobre Ángulo (directo, no tienes que registrarte)
Comentarios
(de más nuevos a más antiguos)
Aún no hay comentarios, ¡deja el primero!









![{displaystyle [0,pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)