Histograma

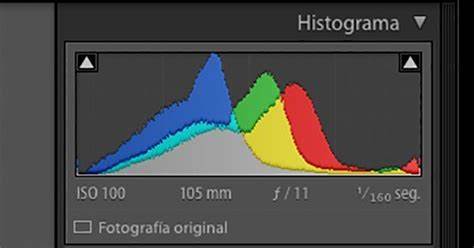
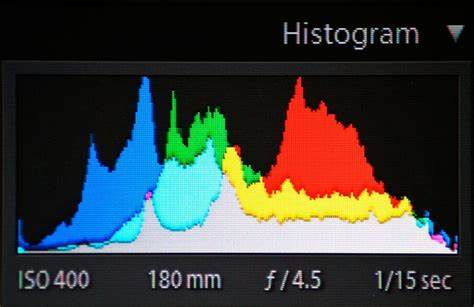
En estadística, un histograma es una representación gráfica de una variable en forma de barras, donde la superficie de cada barra es proporcional a la frecuencia de los valores representados. Sirven para obtener una "primera vista" general, o panorama, de la distribución de la población, o de la muestra, respecto a una característica, cuantitativa y continua (como la longitud o el peso). De esta manera ofrece una visión de grupo permitiendo observar una preferencia, o tendencia, por parte de la muestra o población por ubicarse hacia una determinada región de valores dentro del espectro de valores posibles (sean infinitos o no) que pueda adquirir la característica. Así pues, podemos evidenciar comportamientos, observar el grado de homogeneidad, acuerdo o concisión entre los valores de todas las partes que componen la población o la muestra, o, en contraposición, poder observar el grado de variabilidad, y por ende, la dispersión de todos los valores que toman las partes, también es posible no evidenciar ninguna tendencia y obtener que cada miembro de la población toma por su lado y adquiere un valor de la característica aleatoriamente sin mostrar ninguna preferencia o tendencia.

Se utilizan para relacionar variables cuantitativas continuas. Para variables cuantitativas discretas las barras se dibujan separadas y el gráfico se llama diagrama de frecuencias, porque la variable representada en el eje horizontal ya no representa un espectro continuo de valores, sino valores cuantitativos específicos, igual que ocurre en un diagrama de barras, usado para representar una característica cualitativa o categórica. Su utilidad se hace más evidente cuando se cuenta con un gran número de datos cuantitativos y que se han agrupado en intervalos de clase. Ejemplos de su uso es la representación de edades o estaturas de una población. Por comodidad, sus valores se agrupan en clases, es decir, en intervalos continuos. En los casos en los que los datos son cualitativos (no numéricos), como cierto grado de acuerdo o nivel de estudios, es preferible un diagrama de sectores.

Los histogramas son más frecuentes en ciencias sociales, humanas y económicas que en ciencias naturales y exactas. Y permite la comparación de los resultados de un proceso.

El término "histograma" fue acuñado en 1891 por el matemático estadístico inglés Karl Pearson y es un compuesto de los términos griegos ἱστός (‘histós’, “mástil”) y ɣράμμα ('gramma', "dibujo, figura")^[1]​

Determinar el rango de los datos. Rango es igual al mayor valor menos el menor valor.

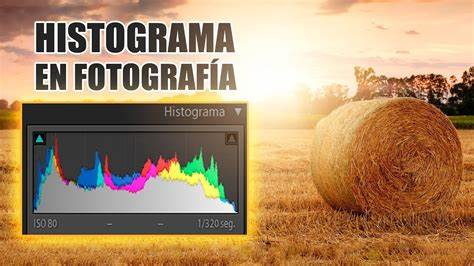
Obtener todos los números de grupos, existen 4 criterios para determinar el número de clases (o barras) –por ejemplo, la regla de Sturges.

Establecer la anchura de clase. Si queremos intervalos iguales tomaremos el rango dividido por el número de clases y comparar con los resultados obtenidos de la dispersión.

Construir los intervalos de clases: Los intervalos resultan de dividir el rango de los datos en segmentos iguales usando la anchura de clase obtenida en el paso 3.

Graficar el histograma: Como todas las clases tienen la misma amplitud las bases de las barras son los intervalos de clases y la altura es la frecuencia de las clases.

El histograma de una imagen representa la frecuencia relativa de los niveles de gris de la imagen. Las técnicas de modificación del histograma de una imagen son útiles para aumentar el contraste de imágenes con histogramas muy concentrados. Sea una imagen de tamaño N×N, la función de distribución del histograma es:

Los histogramas se aplican a variables continuas, aquellas en las que la variable observada (estatura, peso, edad…) pueden tomar cualquier valor real, a veces entre dos valores fijos que determinan su rango. Otros gráficos similares al histograma son los diagramas de barras, que se suelen aplicar a variables discretas y a las cualitativas. A diferencia de las variables continuas aquí los valores intermedios entre dos barras consecutivas no tienen sentido (un dado puede salir 1, 2, 3, 4, 5 o 6, pero no 3,7 ni 5/3) o no pueden observarse (si estudiamos documentos que solo registran edades enteras deberemos tratarla como variable discreta), por eso las barras se dibujan separadas. La distinción entre discreta y continua no siempre es clara. La variable edad se puede considerar continua pues el tiempo es una variable continua, pero frecuentemente se considera como un número entero (la administración no suele considerar edades fraccionarias) y entonces es una variable discreta. Los gráficos estadísticos presentarán el mismo problema, y los mismos datos se podrán representar en diagramas de barras (separadas) si se considera una variable discreta o en histograma (barras unidas) si se considera continua. Incluso la distinción entre cualitativa y cuantitativa puede ser arbitraria, pues muchas cualidades se pueden representar de forma numérica, como hacen los ordenadores. El ejemplo más evidente es el color (ver el ejemplo anterior: histograma de grises), variable claramente cualitativa que los ordenadores traducen a números (por ejemplo usando el código RGB). En las variables cuantitativas y en las cualitativas ordinales es frecuente representar polígonos de frecuencia en lugar de histogramas.

---