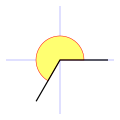
Ãngulo llano
En geometría, el ángulo puede ser definido como la parte del plano determinada por dos semirrectas llamadas lados que tienen el mismo punto de origen llamado vértice del ángulo. La unidad de medida de los ángulos son los grados.
La medida de un ángulo es considerada como la amplitud del arco de circunferencia centrada en el vértice y delimitada por sus lados. Su medida es un múltiplo de la razón entre la longitud del arco y el radio. Su unidad natural es el radián, pero también se puede utilizar el grado sexagesimal o el grado centesimal.
Pueden estar definidos sobre superficies planas (trigonometría plana) o curvas (trigonometría esférica). Se denomina ángulo diedro al espacio comprendido entre dos semiplanos cuyo origen común es una recta. Un ángulo sólido es el que abarca un objeto visto desde un punto dado, midiendo su tamaño aparente.
Ángulo también se utiliza para designar la medición de un ángulo o de una rotación. Esta medida es la relación entre la longitud de un arco circular y su radio. En el caso de un ángulo geométrico, el arco está centrado en el vértice y delimitado por los lados. En el caso de una rotación, el arco está centrado en el centro de la rotación y delimitado por cualquier otro punto y su imagen por la rotación.
La palabra ángulo proviene del latín, angulus, que significa "esquina"; las palabras afines son la griega ἀγκύλος (ankylοs), que significa "torcido, curvado", y la palabra inglés "tobillo". Ambas están conectadas con la raíz Protoindoeuropeo *ank-, que significa "doblarse" o "inclinarse". Nota: ἀγκύλος en lugar de ἀνκύλος es correcto, el γκ es un dígrafo que se pronuncia [ŋk].
Euclides define un ángulo plano como la inclinación recíproca, en un plano, de dos rectas que se encuentran entre sí y no son rectas entre sí. Según Proclus, un ángulo debe ser una cualidad o una cantidad, o una relación. El primer concepto fue utilizado por Eudemo, que consideraba un ángulo como una desviación de una línea recta; el segundo por Carpo de Antioquía, que lo consideraba como el intervalo o espacio entre las líneas que se cruzan; Euclides adoptó el tercer concepto.
Existen básicamente dos formas de definir un ángulo en el plano:
Euclides define un ángulo como la inclinación entre dos líneas que se encuentran una a otra en un plano y no están en línea recta. Según Proclo, un ángulo debe ser una calidad o una cantidad, o una relación. El primer concepto fue utilizado por Eudemo de Rodas, que describió un ángulo como desviación de una línea recta; el segundo por Carpo de Antioquía, que lo vio como el intervalo o el espacio entre las líneas que se intersecaban; Euclides adoptó un tercer concepto, aunque sus definiciones de ángulos rectos, agudos, y obtusos son cuantitativas.
Se denomina región angular a cada una de las dos partes en que queda dividido el plano por un ángulo.
Se llama amplitud de un ángulo a la medida de este.
Las unidades utilizadas para la medida de los ángulos del plano son:
Los ángulos se pueden medir mediante utensilios tales como el goniómetro, el cuadrante, el sextante, la ballestina, el transportador de ángulos o semicírculo graduado, graduador, etc.
Aunque la definición de la medida de un ángulo no respalda el concepto de ángulo negativo, con frecuencia es útil imponer una convención que permita que los valores angulares positivos y negativos representen orientaciones y / o rotaciones en direcciones opuestas con respecto a alguna referencia.
En un sistema de coordenadas cartesiano bidimensional, un ángulo se define típicamente por sus dos lados, con su vértice en el origen. El lado inicial está en el eje "x" positivo, mientras que el otro lado o lado terminal está definido por la medida del lado inicial en radianes, grados o vueltas. Con ángulos positivos que representan rotaciones hacia el eje "y" positivo y ángulos negativos que representan rotaciones hacia el eje "y" negativo. Cuando las coordenadas cartesianas están representadas por la posición estándar, definida por el eje "x" hacia la derecha y el eje "y" eje hacia arriba, las rotaciones positivas son en sentido antihorario y las rotaciones negativas son en sentido horario.
En muchos contextos, un ángulo de -θ es efectivamente equivalente a un ángulo de "una vuelta completa menos θ". Por ejemplo, una orientación representada como -45 ° es efectivamente equivalente a una orientación representada como 360° -45 ° o 315°. Aunque la posición final es la misma, una rotación física (movimiento) de -45° no es lo mismo que una rotación de 315° (por ejemplo, la rotación de una persona sosteniendo una escoba descansando sobre un piso polvoriento dejaría huellas visualmente diferentes de regiones barridas en el suelo).
En la geometría tridimensional, "en el sentido de las agujas del reloj" y "en el sentido contrario a las agujas del reloj" no tienen un significado absoluto, por lo que la dirección de los ángulos positivos y negativos debe definirse en relación con alguna referencia, que suele ser un vector que pasa por el vértice del ángulo y es perpendicular al plano en donde se encuentran los rayos del ángulo.
En la navegación, los rumbos o acimut se miden en relación con el norte. Por convención, visto desde arriba, los ángulos de orientación son positivos en el sentido de las agujas del reloj, por lo que una orientación de 45° corresponde a una orientación noreste. Los rumbos negativos no se utilizan en la navegación, por lo que una orientación noroeste corresponde a un rumbo de 315°.
Los ángulos, de acuerdo con su amplitud, reciben estas denominaciones:
Es decir, mayor de 0° y menor de 90° (grados sexagesimales), o menor de 100g (grados centesimales).
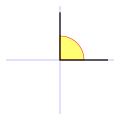
Es equivalente a 90° sexagesimales (o 100g centesimales).
Los dos lados de un ángulo recto son perpendiculares entre sí.
La proyección ortogonal de uno sobre otro es un punto, que coincide con el vértice.
Mayor a 90° y menor a 180° sexagesimales (o más de 100g y menos de 200g centesimales).
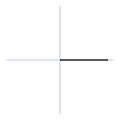
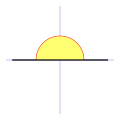
Equivalente a 180° sexagesimales (o 200g centesimales).
Los ángulos agudos y obtusos son ángulos oblicuos.
Equivalente a 360° sexagesimales (o 400g centesimales).
Se llama así a los ángulos que tienen el mismo lado final. Pueden ser en rotación contraria al ángulo dado o con una rotación mayor de 360°.
En un plano, dos semirrectas (no coincidentes ni alineadas) con un origen común determinan siempre dos ángulos, uno convexo (el de menor amplitud) y otro cóncavo (el de mayor amplitud):
Equivale a más de 0° y menos de 180°sexagesimales (o más de 0g y menos de 200g centesimales).
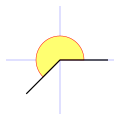
Esto es, más de 180° y menos de 360° sexagesimales (o más de 200g y menos de 400g centesimales).
Denominación relativo a su posición:
Denominación en función de la suma de su amplitud:
Cuando dos rectas son cortadas por una tercera, se forman las siguientes relaciones distantes:
Son los obtenidos mediante la suma o diferencia de ángulos. En la figura se representan dos sectores circulares contiguos, cada uno con su ángulo, denominados α y β respectivamente; la unión de los dos sectores tendrá por ángulo la composición, en este caso la suma, α + β, de los ángulos de los sectores que unimos.
Las razones trigonométricas de los ángulos compuestos están relacionadas con la de los ángulos componentes mediante las fórmulas de razones trigonométricas de ángulos compuestos, ver por ejemplo Identidades trigonométricas.
Un ángulo que forma parte de un polígono simple se llama ángulo interior si se encuentra en el interior de ese polígono simple, siendo formado por lados adyacentes. Un polígono cóncavo simple tiene al menos un ángulo interior que es un ángulo reflejo. En geometría euclidiana , las medidas de los ángulos interiores de un triángulo suman π radianes, 180 ° o 1/2 vuelta; las medidas de los ángulos interiores de un cuadrilátero convexo simple suman 2 π radianes, 360 ° o 1 vuelta. En general, las medidas de los ángulos interiores de un polígono convexo simple con n lados suman (n - 2)π radianes, o ( n - 2) 180 grados, ( n - 2) 2 ángulos rectos o ( n - 2) 1/ 2 vuelta.
Un ángulo, respecto de una circunferencia, pueden ser:
Ángulo central, si tiene su vértice en el centro de esta.
Ángulo inscrito, si su vértice es un punto de la circunferencia y sus lados la cortan en dos puntos.
Ángulo semi-inscrito, si su vértice está sobre esta, uno de sus lados la corta y el otro es tangente, siendo el punto de tangencia el propio vértice.
Ángulo interior, si su vértice está en el interior de la circunferencia.
Ángulo exterior, si tiene su vértice en el exterior de esta.
La trisección del ángulo es un problema clásico que consiste en dividir un ángulo dado en tres partes iguales usando solo regla y compás. En general, es imposible de resolver con esas condiciones.
Dado un espacio vectorial, cuyo cuerpo es el conjunto de los números reales y en el que existe un producto escalar entre vectores , se define el ángulo formado por dos vectores no nulos e mediante la expresión:
Si el cociente anterior es 0, se dice que ambos vectores son ortogonales o perpendiculares. El cociente anterior está en el intervalo debido a la desigualdad de Cauchy-Schwarz, lo que garantiza que siempre puede aplicarse el arcocoseno. Normalmente, se toma la rama del arcocoseno de forma que el ángulo que forman dos vectores siempre está en el intervalo (geométricamente, se elige el menor de los ángulos que forman dos vectores). Las principales propiedades que cumple el ángulo de dos vectores son las siguientes:
![{displaystyle [0,pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)
El tamaño de un ángulo geométrico se suele caracterizar por la magnitud de la menor rotación que mapea uno de los rayos en el otro. Se dice que los ángulos que tienen el mismo tamaño son iguales o congruentes o de igual medida.
En algunos contextos, como la identificación de un punto en un círculo o la descripción de la orientación de un objeto en dos dimensiones con respecto a una orientación de referencia, los ángulos que difieren en un múltiplo exacto de una vuelta completa son efectivamente equivalentes. En otros contextos, como la identificación de un punto en una curva espiral o la descripción de la rotación acumulada de un objeto en dos dimensiones con respecto a una orientación de referencia, los ángulos que difieren en un múltiplo no nulo de una vuelta completa no son equivalentes.
Para medir un ángulo θ, se traza un arco de círculo centrado en el vértice del ángulo, por ejemplo, con un par de compases. El cociente de la longitud s del arco por el radio r del círculo es el número de radianes del ángulo. Convencionalmente, en matemáticas y en el SI, el radián se trata como si fuera igual al valor adimensional 1.
El ángulo expresado en otra unidad angular puede obtenerse entonces multiplicando el ángulo por una constante de conversión adecuada de la forma k2π, donde k es la medida de una vuelta completa expresada en la unidad elegida (por ejemplo, k = 360° para grados o 400 grad para gradians):
El valor de θ así definido es independiente del tamaño del círculo: si se cambia la longitud del radio, entonces la longitud del arco cambia en la misma proporción, por lo que la relación s/r no se altera.
El postulado de adición de ángulos establece que si B está en el interior del ángulo AOC, entonces
La medida del ángulo AOC es la suma de la medida del ángulo AOB y la medida del ángulo BOC.
Las unidades utilizadas para representar ángulos se enumeran a continuación en orden de magnitud descendente. De estas unidades, el grado y el radián son, con mucho, las más utilizadas. Los ángulos expresados en radianes son adimensionales para el análisis dimensional.
La mayoría de las unidades de medida angular se definen de forma que un giro (es decir, un círculo completo) es igual a n unidades, para algún número entero n. Las dos excepciones son el radián (y sus submúltiplos decimales) y la parte del diámetro.
Este artículo incorpora texto de una publicación sin restricciones conocidas de derecho de autor: 
Varios autores (1910-1911). «Angle». En Chisholm, Hugh, ed. Encyclopædia Britannica. A Dictionary of Arts, Sciences, Literature, and General information (en inglés) (11.ª edición). Encyclopædia Britannica, Inc.; actualmente en dominio público.