Función W de Lambert

En matemáticas, la función W de Lambert, denominada así en honor a Johann Heinrich Lambert, si bien también se conoce como función Omega o log producto, es la función inversa de f(w) = we^w donde e^w es la función exponencial natural y w es cualquier número complejo. La función se define mediante W. Para todo número complejo denominado z, se tiene:

${displaystyle z=W(z)e^{W(z)}.}$

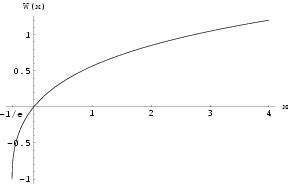
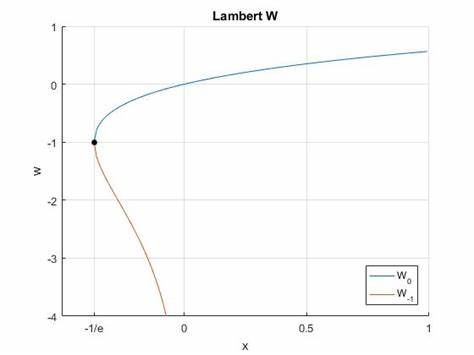
Puesto que la función f no es inyectiva, la función W es multivaluada (excepto en 0). De restringir los argumentos reales, x y w reales, la función es definida solo por x ≥ −1/e, y es doble-valuada en (−1/e, 0); la restricción adicional w ≥ −1 define una función simple-valuada W₀(x), representable gráficamente. Tenemos W₀(0) = 0 y W₀(−1/e) = −1. La rama alternativa en [−1/e, 0) con w ≤ −1 es indicada como W₋₁(x) y decrece de W₋₁(−1/e) = −1 a W₋₁(0⁻) = −∞.

La función W de Lambert no puede expresarse en términos de funciones elementales. Es útil en combinatoria, por ejemplo en la enumeración de árboles. Puede emplearse para resolver varias ecuaciones que alberguen exponenciales y también participa en la solución de ecuaciones diferenciales retrasadas temporalmente, como y'(t) = a y(t − 1).

Si x es real pero mayor o igual que ${displaystyle -e^{-1}}$, o si x es complejo o imaginario puro, entonces:

${displaystyle W(x)={frac {x}{2pi }}int _{-pi }^{pi }{frac {(1-vcot v)^{2}+v^{2}}{x+vcsc vcdot e^{-vcot v}}}{ m {d}}v,}$

Si ${displaystyle {mathfrak {R}}(x)<-e^{-1},{mathfrak {I}}(x)leq -e^{-1}}$，

${displaystyle W(x)=1+(ln x-1)e^{-{frac { m {i}}{2pi }}int _{0}^{infty }{frac {1}{1+t}}ln {frac {ln x+t-ln t-{ m {i}}pi }{ln x+t-ln t+{ m {i}}pi }}{ m {d}}t},}$

La función ${displaystyle W_{k}(x)}$ equivale a la siguiente integral:

${displaystyle W_{k}(x)=1+(ln x+2kpi {{ m {i}}-1)e^{-{frac { m {i}}{2pi }}int _{0}^{infty }{frac {1}{t+1}}ln {frac {ln x+t-ln t+(2k-1){ m {i}}pi }{ln x+t-ln t+(2k+1){ m {i}}pi }}{ m {d}}t}},}$

，

donde ${displaystyle xin {mathbb {R} -(-e^{-1};0)},kin mathbb {Z} ,}$

Lambert inicialmente postuló una función relacionada (la ecuación trascendental de Lambert) en 1758,^[1]​ que dio lugar a un artículo de Leonhard Euler en 1783 en el cual se discutía el caso especial we^w. Sin embargo, la inversa de we^w fue descrita por Polya y Szegö en 1925. La función de Lambert fue "redescubierta" alrededor de una vez por década en aplicaciones especializadas, pero su importancia no se apreció realmente hasta la década de 1990. Cuando se anunció que la función W de Lambert da una solución exacta a los valores propios de la energía del sistema cuántico correspondiente al modelo descrito por el operador de Dirac para duplicar así para el caso de igualdad de cargas - un problema físico fundamental - Corless y los desarrolladores del sistema Maple hicieron una búsqueda bibliográfica y descubrieron que esta función aparece en todas partes en las aplicaciones prácticas.^[2]​

Por derivación implícita, se encuentra que W satisface la ecuación diferencial ordinaria.

${displaystyle z(1+W){frac {dW}{dz}}=Wquad mathrm {para } z eq -1/e,,}$

por lo tanto:

${displaystyle {frac {dW}{dz}}={frac {W(z)}{z(1+W(z))}}quad mathrm {para } z eq -1/e,.}$

La función W (x), y algunas expresiones que implican a W(x), pueden ser integradas empleando la regla de sustitución w = W(x), i.e. x = w e^w:

${displaystyle int W(x),dx=xleft(W(x)-1+{frac {1}{W(x)}} ight)+C}$

Las series de Taylor de W₀ en torno a 0 pueden ser resueltas mediante el teorema de inversión de Lagrange que procede de:

${displaystyle forall |x|<e^{-1}:W_{0}(x)=sum _{n=1}^{infty }{frac {(-n)^{n-1}}{n!}} x^{n}=x-x^{2}+{frac {3}{2}}x^{3}-{frac {8}{3}}x^{4}+{frac {125}{24}}x^{5}-cdots }$

El radio de convergencia es 1/e, como puede verse mediante el criterio de d'Alembert. La función definida por las series puede extenderse a una función holomórfica definida para todos los números complejos con un corte de rama en torno al intervalo (−∞, −1/e]; la mencionada función holomórfica define la rama principal de la función W de Lambert.

Algunas ecuaciones que poseen exponenciales pueden resolverse mediante esta función. Para ello, la estrategia general consiste en sustituir todas las instancias de lo desconocido a una parte de la ecuación y tornarla, entonces, a la forma Y = Xe^X, para la cual W proporciona una solución.

Es decir:

${displaystyle X=Ye^{Y};Longleftrightarrow ;Y=W(X)}$

De forma más general, la ecuación

donde

puede transformarse mediante la sustitución

en

dando

que se resuelve como

Técnicas similares llevan a

con solución

o, de forma equivalente,

Siempre que el exponencial complejo infinito tipo tetración

converja, la función W de Lambert proporciona un valor límite como

en el cual ln(z) denota la rama principal de la función logarítmica compleja.

Las soluciones para

poseen la forma

La solución para la corriente eléctrica en circuitos diodo/resistencia puede escribirse como una función W.

La ecuación diferencial retrasada

posee la ecuación característica ${displaystyle lambda =ae^{-lambda }}$, que lleva a ${displaystyle lambda =W_{k}(a)}$ y ${displaystyle y(t)=e^{W_{k}(a)t}}$, donde ${displaystyle k}$ es el índice de la rama. Si ${displaystyle a}$ es real, sólo debe considerarse ${displaystyle W_{0}(a)}$.

La función W de Lambert abastece de soluciones reales a las ecuaciones "algébricas-transcendentales" (de eso x) de la forma:

o a₀, c y r son constantes reales. La solución es ${displaystyle x=r+W(ce^{-cr}/a_{o})/c}$. Las generalizaciones de la función W de Lambert^[3]​^[4]​^[5]​ incluye:

Las aplicaciones de la función W de Lambert en los problemas de la física fundamental hasta no son agotadas para el caso estándar exprimido en (1), como se acaba de verlo en los dominios de la física atómica y molecular, así como en óptica.^[9]​

La función W puede evaluarse mediante la relación de recurrencia

${displaystyle w_{j+1}=w_{j}-{frac {w_{j}e^{w_{j}}-z}{e^{w_{j}}(w_{j}+1)-{frac {(w_{j}+2)(w_{j}e^{w_{j}}-z)}{2w_{j}+2}}}}}$

proporcionada en Corless et al. para calcular W. Junto con la estima de evaluación de error de Chapeau-Blondeau y Monir. Esto calcula la rama principal para ${displaystyle x>-1/e}$.

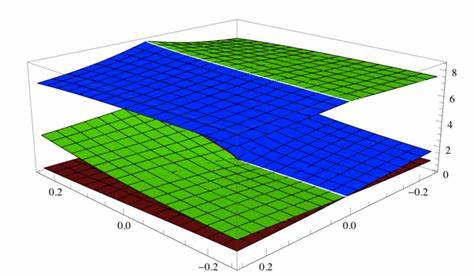
z = Re(W₀(x + i y))

z = Im(W₀(x + i y))

W₀(x + i y)

---