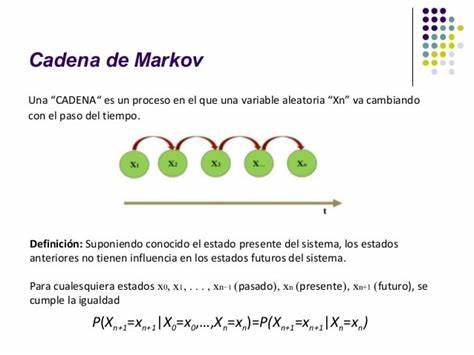
Cadena de Márkov

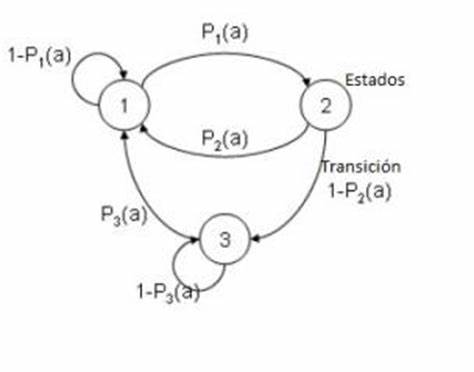
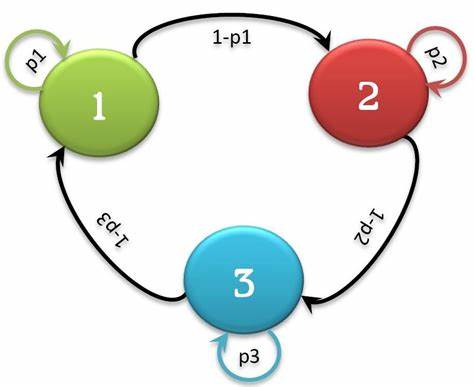
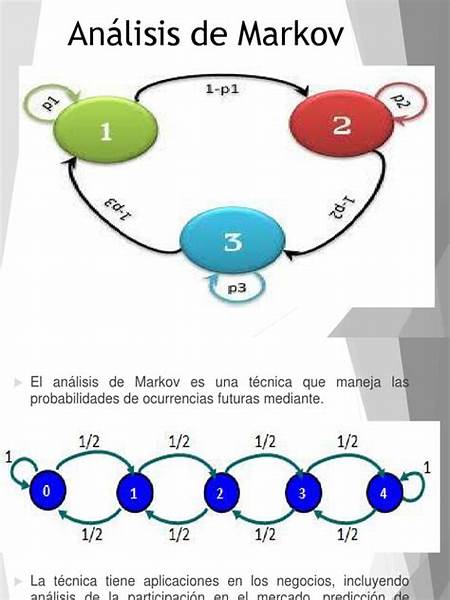
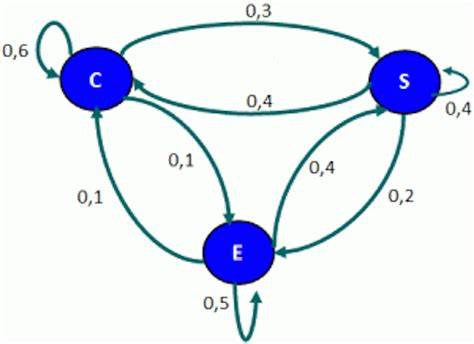
En la teoría de la probabilidad, se conoce como cadena de Márkov o modelo de Márkov a un tipo especial de proceso estocástico discreto en el que la probabilidad de que ocurra un evento depende solamente del evento inmediatamente anterior. Esta característica de falta de memoria recibe el nombre de propiedad de Markov.

Recibe su nombre del matemático ruso Andréi Márkov (1856-1922), que lo introdujo en 1906.^[1]​

Estos modelos estadísticos cuentan con un gran número de aplicaciones reales.

En matemáticas, una Cadena de Markov es un proceso estocástico a tiempo discreto ${displaystyle {X_{n}:n=0,1,2dots }}$ con espacio de estados discreto ${displaystyle S}$ que para cualquier entero ${displaystyle ngeq 0}$ y para cualesquiera ${displaystyle x_{0},x_{1},dots ,x_{n+1}in S}$ satisface

a esta propiedad se le conoce como propiedad de Markov.

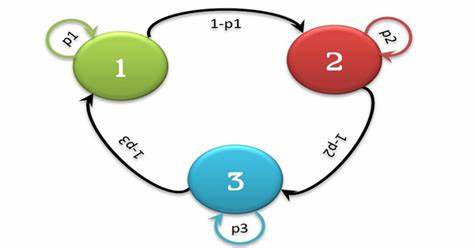
Se dice que una Cadena de Markov es homogénea si la probabilidad de ir del estado ${displaystyle i}$ al estado ${displaystyle j}$ en un paso no depende del tiempo en el que se encuentra la cadena, esto es:

para todo ${displaystyle ngeq 0}$ y para cualquier ${displaystyle i,jin S}$.

Si para alguna pareja de estados y para algún tiempo ${displaystyle n}$ la propiedad antes mencionada no se cumple entonces diremos que la Cadena de Markov es no homogénea.

Sean ${displaystyle i}$ y ${displaystyle j}$ dos estados de una Cadena de Markov, a la probabilidad de ir del estado ${displaystyle i}$ en el tiempo ${displaystyle n}$ al estado ${displaystyle j}$ en el tiempo ${displaystyle n+1}$ se denota por

y cuando la cadena es homogénea, se denota por

que representa la probabilidad de pasar del estado ${displaystyle i}$ al estado ${displaystyle j}$ en una unidad de tiempo.

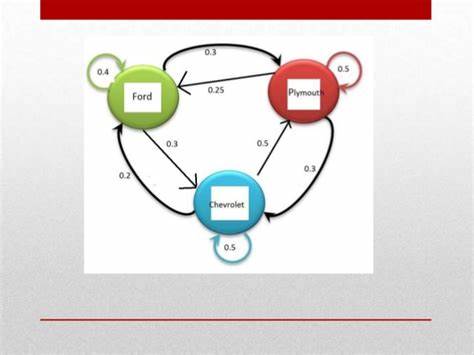
Teniendo las probabilidades de transición en un paso ${displaystyle p_{ij}}$, si variamos los índices ${displaystyle i,j}$ sobre el espacio de estados ${displaystyle S={0,1,2,dots }}$ obtenemos la matriz ${displaystyle P}$ llamada matriz de probabilidades de transición en un paso, es decir

donde la entrada ${displaystyle (i,j)}$ representa la probabilidad de pasar del estado ${displaystyle i}$ al estado ${displaystyle j}$ en un paso.

La matriz ${displaystyle P}$ esta es una matriz estocástica pues satisfcae

Similarmente se define la matriz de probabilidades de transición en ${displaystyle n}$ pasos, esta se denota por ${displaystyle P(n)}$ y está dada por

donde la entrada ${displaystyle (i,j)}$ representa la probabilidad de pasar del estado ${displaystyle i}$ al estado ${displaystyle j}$ en ${displaystyle n}$ pasos.

Para cualesquiera ${displaystyle r,nin mathbb {Z} }$ tales que ${displaystyle 0leq rleq n}$ y para cualesquiera estados ${displaystyle i,jin S}$ se cumple

Como consecuencia de este resultado, la probabilidad de transición en ${displaystyle n}$ pasos, ${displaystyle p_{ij}(n)}$, está dada por la entrada ${displaystyle (i,j)}$ de la ${displaystyle n}$-ésima potencia de la matriz de probabilidades de transición en un paso, es decir

Con lo anterior, el problema de calcular las probabilidades de transición en ${displaystyle n}$ pasos se convierte en halla la ${displaystyle n}$-ésima potencia de la matriz de probabilidades de transición en un paso, esto es

Para dos estados ${displaystyle i}$ y ${displaystyle j}$ en el espacio de estados ${displaystyle S}$, diremos que el estado ${displaystyle j}$ es accesible desde el estado ${displaystyle i}$ y escribiremos ${displaystyle i ightarrow j}$ si ${displaystyle exists ,nin mathbb {Z} ^{+}}$ tal que

si ${displaystyle i ightarrow j}$ y ${displaystyle j ightarrow i}$ entonces diremos que el estado ${displaystyle i}$ se comunica con el estado ${displaystyle j}$ y escribiremos ${displaystyle ilongleftrightarrow j}$.

La propiedad "${displaystyle longleftrightarrow }$" es una relación de equivalencia. Esta relación induce una partición del espacio de estados. A estas clases de equivalencia las llamaremos clases de comunicación.

Dado un estado ${displaystyle iin S}$, denotaremos a su clase de comunicación como ${displaystyle C(i)}$, por lo que ${displaystyle ilongleftrightarrow j}$ si y sólo si ${displaystyle C(i)=C(j)}$.

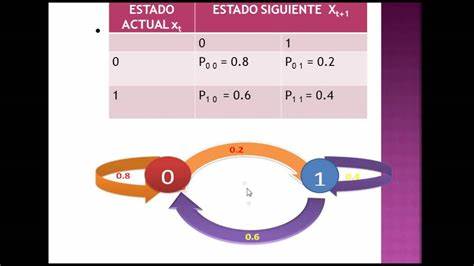
Si ${displaystyle C(i)=S}$ entonces se dice que la cadena es irreducible.

El periodo de un estado ${displaystyle iin S}$ se define como:

donde ${displaystyle { m {mcd}}}$ denota el máximo común divisor.

Una cadena de Márkov se dice aperiódica si todos sus estados son aperiódicos, es decir, si ${displaystyle d(i)=1quad forall ;iin S}$.

Si ${displaystyle Csubset S}$, definimos el tiempo de primera visita a ${displaystyle C}$ como la variable aleatoria

esto es, ${displaystyle au _{C}}$ denota la primera vez que la cadena entra al conjunto de estados ${displaystyle C}$.

Se define

como la probabilidad de que una cadena que inicia en el estado ${displaystyle i}$ llegue al estado ${displaystyle j}$ por primera vez en ${displaystyle n}$ pasos, donde ${displaystyle f_{ij}(0)=0}$.

En particular, cuando ${displaystyle i=j}$, ${displaystyle f_{ii}(n)}$ denota la probabilidad de regresar por primera vez al estado ${displaystyle i}$ en ${displaystyle n}$ pasos.

Y se definen

como la probabilidad de una eventual visita a partir del estado ${displaystyle i}$ al estado ${displaystyle j}$ y

como la probabilidad de regresar partir del estado ${displaystyle i}$ y regresar a él mismo en un tiempo finito.

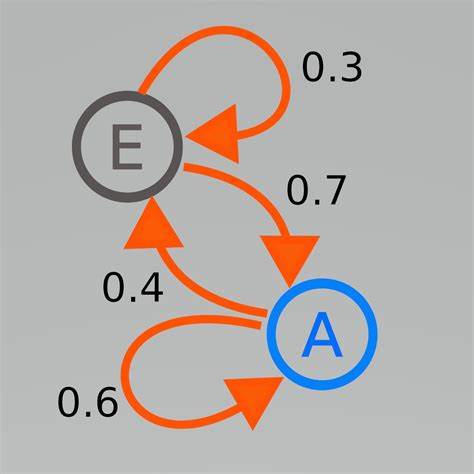
En una cadena de Markov con espacio de estados ${displaystyle S}$, diremos que:

o utilizando las probabilidades de transición en ${displaystyle n}$ pasos:

La recurrencia es una propiedad de clase pues

Se define como el tiempo medio de recurrencia de un estado recurrente ${displaystyle j}$ a partir del estado ${displaystyle i}$ como la esperanza de

y se denota por ${displaystyle mu _{ij}}$

Esta esperanza representa el número de pasos promedio que a la cadena le toma regresar al estado recurrente ${displaystyle j}$.

En particular, cuando ${displaystyle i=j}$ escribimos ${displaystyle mu _{i}}$ en lugar de ${displaystyle mu _{ii}}$.

Se dice que un estado recurrente ${displaystyle i}$ es

La recurrencia positiva es una propiedad de clase pues

Se dice que el vector ${displaystyle pi =(pi _{0},pi _{1},dots )}$ es una distribución de probabilidad si

Se dice que una distribución de probabilidad ${displaystyle pi =(pi _{0},pi _{1},dots )}$ es estacionaria para una Cadena de Markov con matriz de probabilidades de transición ${displaystyle P=(p_{ij})}$ si

En forma matrícula lo anterior es equivalente a ${displaystyle pi =pi P}$ y significa que si una variable aleatoria inicial ${displaystyle X_{0}}$ tiene una distribución ${displaystyle pi }$ entonces la distribución de ${displaystyle X_{n}}$ también es ${displaystyle pi }$, es decir, esta distribución no cambia con el paso del tiempo.

Para encontrar una posible distribución estacionaria de una cadena con matriz ${displaystyle P}$, un método consiste en resolver el sistema de ecuaciones

La distribución estacionaria puede no ser única o incluso no existir.

Si una Cadena de Markov es irreducible y recurrente positiva entonces tiene una única distribución estacionaria y esta está dada por

donde ${displaystyle mu _{j}}$ es el tiempo medio de recurrencia del estado ${displaystyle j}$.

Si una cadena de Markov es

entonces para cualesquiera ${displaystyle i,jin S}$

Si una cadena de Markov es

entonces las probabilidades límite

existen, están dadas por

y constituyen la única solución al sistema de ecuaciones

Una cadena de Markov se dice irreducible si se cumple cualquiera de las siguientes condiciones (equivalentes entre sí):

La cadena de Ehrenfest o la caminata aleatoria sin barreras absorbentes son ejemplos de cadenas de Márkov irreducibles.

Una cadena de Markov se dice recurrente positiva si todos sus estados son recurrentes positivos. Si la cadena es además irreducible es posible demostrar que existe un único vector de probabilidad invariante y está dado por:

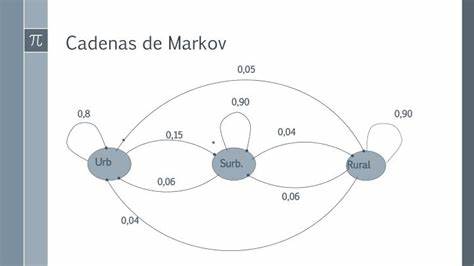
Una cadena de Márkov se dice regular (también primitiva o ergódica) si existe alguna potencia positiva de la matriz de transición cuyas entradas sean todas estrictamente mayores que cero.

Cuando el espacio de estados ${displaystyle S}$ es finito, si ${displaystyle P}$ denota la matriz de transición de la cadena se tiene que:

donde ${displaystyle W}$ es una matriz con todos sus renglones iguales a un mismo vector de probabilidad w, que resulta ser el vector de probabilidad invariante de la cadena. En el caso de cadenas regulares, este vector invariante es único.

Una cadena de Márkov con espacio de estados finito se dice absorbente si se cumplen las dos condiciones siguientes:

Si denotamos como A al conjunto de todos los estados absorbentes y a su complemento como D, tenemos los siguientes resultados:

donde la submatriz Q corresponde a los estados del conjunto ${displaystyle D}$, ${displaystyle I}$ es la matriz identidad, ${displaystyle 0}$ es la matriz nula y ${displaystyle R}$ alguna submatriz.

Si en lugar de considerar una secuencia discreta ${displaystyle X_{1},X_{2},dots ,X_{i},dots }$ con ${displaystyle i}$ indexado en el conjunto ${displaystyle mathbb {N} ;!}$ de números naturales, se consideran las variables aleatorias ${displaystyle X_{t}}$ con ${displaystyle t}$ que varía en un intervalo continuo del conjunto ${displaystyle mathbb {R} ;!}$ de números reales, tendremos una cadena en tiempo continuo. Para este tipo de cadenas en tiempo continuo la propiedad de Márkov se expresa de la siguiente manera:

Para una cadena de Márkov continua con un número finito de estados puede definirse una matriz estocástica dada por:

La cadena se denomina homogénea si ${displaystyle mathbf {P} (t_{1},t_{2})=mathbf {P} (t_{2}-t_{1})}$. Para una cadena de Márkov en tiempo continuo homogénea y con un número finito de estados puede definirse el llamado generador infinitesimal como:^[2]​

Y puede demostrarse que la matriz estocástica viene dada por:

Si consideramos el tiempo atmosférico de una región a través de distintos días, es posible asumir que el estado actual solo depende del último estado y no de toda la historia en sí, de modo que se pueden usar cadenas de Markov para formular modelos climatológicos básicos. Por ejemplo, se han desarrollado modelos de recurrencia de las lluvias basados en cadenas de Markov.^[3]​

Una importante aplicación de las cadenas de Markov se encuentra en el proceso Galton-Watson. Este es un proceso de ramificación que se puede usar, entre otras cosas, para modelar el desarrollo de una epidemia (véase modelaje matemático de epidemias).

El pagerank de una página web (usado por Google en sus motores de búsqueda) se define a través de una cadena de Markov, donde la posición que tendrá una página en el buscador será determinada por su peso en la distribución estacionaria de la cadena.

Las cadenas de Márkov son utilizadas para proveer una solución analítica a ciertos problemas de simulación, por ejemplo en teoría de colas el Modelo M/M/1^[4]​ es de hecho un modelo de cadenas de Markov.

Son muchos los juegos de azar que se pueden modelar a través de una cadena de Márkov. El modelo de la ruina del jugador, (Gambler's ruin), que establece la probabilidad de que una persona que apuesta en un juego de azar finalmente termine sin dinero, es una de las aplicaciones de las cadenas de Márkov en este rubro.

Las cadenas de Márkov se pueden utilizar en modelos simples de valuación de opciones para determinar cuándo existe oportunidad de arbitraje, así como en el modelo de colapsos de una bolsa de valores o para determinar la volatilidad de los precios. En los negocios, las cadenas de Márkov se han utilizado para analizar los patrones de compra de los deudores morosos, para planear las necesidades de personal y para analizar el reemplazo de equipo.

Se emplean cadenas de Márkov en teoría de genética de poblaciones, para describir el cambio de frecuencias génicas en una población pequeña con generaciones discretas, sometida a deriva genética. Ha sido empleada en la construcción del modelo de difusión de Motō Kimura.

Diversos algoritmos de composición musical usan cadenas de Márkov, por ejemplo el software Csound o Max. Uno de los compositores que usó esta técnica en sus composiciones fue Iannis Xenakis con su obra Analoguique A et B (1958–59).

Se emplean cadenas de Márkov en inventarios, mantenimiento y flujo de proceso.

Se utilizan en las máquinas de Boltzmann.

---