Polígono regular
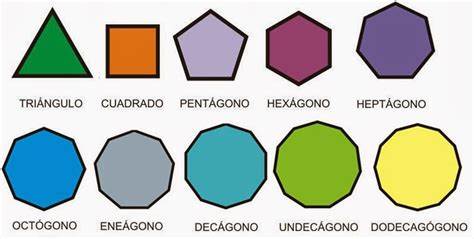
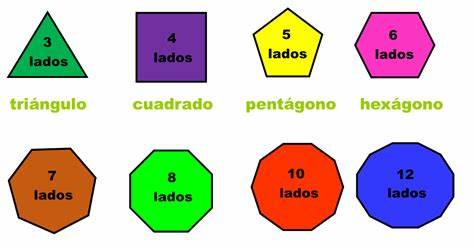
En geometría plana, se denomina polígono regular a un polígono cuyos lados y ángulos interiores son iguales entre sí. Los polígonos regulares de tres y cuatro lados se llaman triángulo equilátero y cuadrado, respectivamente. Para polígonos de más lados, se añade el adjetivo regular (pentágono regular, hexágono regular, octágono regular, etc). Solo algunos polígonos regulares pueden ser construidos con regla y compás.
Observación: A medida que crece el número de lados de un polígono regular, se asemeja más a una circunferencia.
Existen diversas fórmulas para calcular el área de un polígono regular, dependiendo de los elementos conocidos.
El área de un polígono regular, conociendo el perímetro y la apotema es:
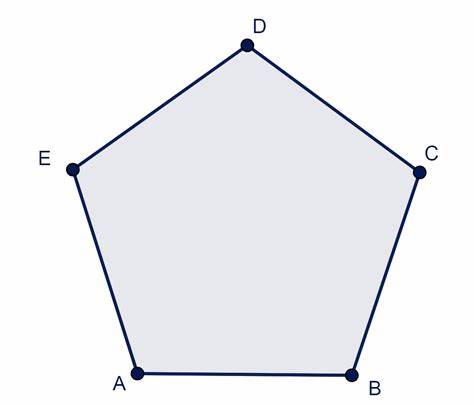
O de otro modo
el área es igual al producto de apotema: a por semiperímetro: p.
Sabiendo que:
Además , ya que es la mitad de un ángulo central (esto en radianes).
Observando la imagen, es posible deducir que:
Sustituyendo el lado:

Finalmente:
Con esta fórmula se puede averiguar el área con el número de lados y la apotema, sin necesidad de recurrir al perímetro.
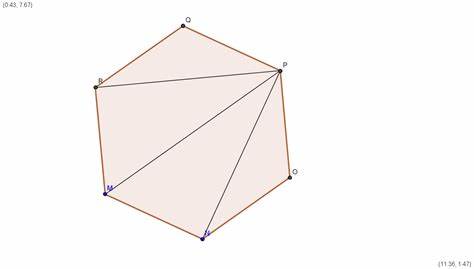
Un polígono queda perfectamente definido por su número de lados n, y el radio r, por tanto podemos determinar cual es su área, a la vista de la figura, tenemos que:
donde el ángulo central es:
sabiendo que el área de un polígono es:
y sustituyendo el valor del lado y la apotema calculados antes, tenemos:
ordenando tenemos:
sabiendo que:
resulta:
o lo que es lo mismo:
Con esta expresión podemos calcular el área del polígono, conociendo solamente el número de lados y su radio, lo que resulta útil en muchos casos.
si queremos expresar el área en función del lado, podemos calcularlo de la siguiente manera:
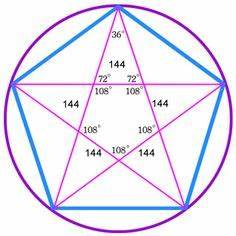
Sea el ángulo formado por el Lado "L" y el radio "r":
El valor de la apotema en función del lado será, por la definición de la tangente:
Despejando la apotema tenemos:
Sustituimos la apotema por su valor:
Se puede ver en el dibujo que y la fórmula puede escribirse también como .
Con lo que conociendo el número de lados del polígono regular y la longitud del lado podemos calcular su superficie.
La apotema, , de un polígono regular de lados de longitud viene dada por
O bien, en función del circunradio, ,
La sagita, , de un polígono regular de lados de longitud viene dada por
O bien, en función del circunradio,
Para determinar el número de diagonales Nd, de un polígono de n vértices realizaremos el siguiente razonamiento:
Según el razonamiento tendremos que:
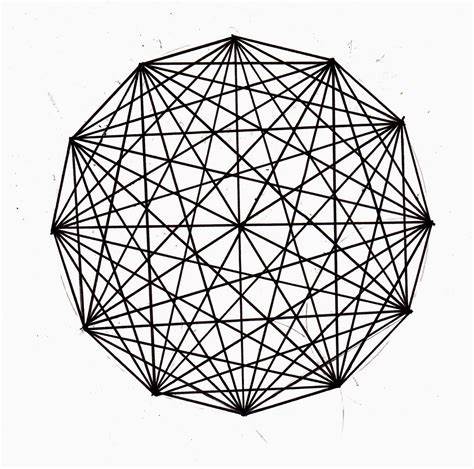
La diagonal más pequeña de un polígono regular es la que une dos vértices alternos, para determinar su longitud, partimos del ángulos central y del radio, el radio que pasa por el vértice intermedio, corta a la diagonal en el punto A, este radio y la diagonal son perpendiculares en A.
Esto es el triángulo VAC es rectángulo en A, por tanto:
que resulta:
de donde deducimos que:
Sabiendo el valor del ángulo central:
La diagonal más pequeña de un polígono regular, solo depende del radio y del número de lados, siendo tanto mayor cuanto mayor sea el radio y disminuyendo de longitud cuando aumenta el número de lados del polígono.
En general la longitud de las diagonales de un polígono regular viene dada por la relación de recurrencia
Escribe un comentario o lo que quieras sobre Polígono regular (directo, no tienes que registrarte)
Comentarios
(de más nuevos a más antiguos)
Aún no hay comentarios, ¡deja el primero!








