Función gamma

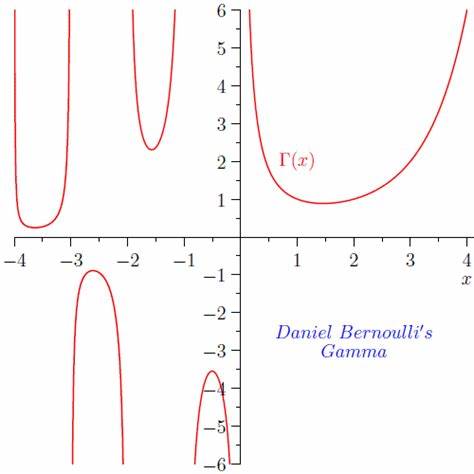
En matemáticas, la función gamma (denotada como ${displaystyle Gamma (z)}$, donde ${displaystyle Gamma }$ es la letra griega gamma en mayúscula), es una aplicación que extiende el concepto de factorial a los números reales y complejos. La notación fue propuesta por Adrien-Marie Legendre. Si la parte real del número complejo ${displaystyle z}$ es positiva, entonces la integral

converge absolutamente; esta integral puede ser extendida a todo el plano complejo, excepto a los enteros negativos y al cero. Si ${displaystyle nin mathbb {Z} ^{+}}$ entonces

lo que nos muestra la relación de esta función con el factorial. De hecho, la función gamma extiende el concepto de factorial a cualquier valor complejo de ${displaystyle z}$. La función gamma aparece en varias funciones de distribución de probabilidad, por lo que es bastante usada tanto en probabilidad y estadística como en combinatoria.

La notación ${displaystyle Gamma (z)}$ se debe a Legendre. Si la parte real del número complejo ${displaystyle z}$ es estrictamente positiva ${displaystyle left({ ext{Re}}(z)>0 ight)}$, entonces la integral

converge absolutamente y es conocida como integral de Euler de segundo orden. Utilizando integración por partes se obtiene la siguiente propiedad:

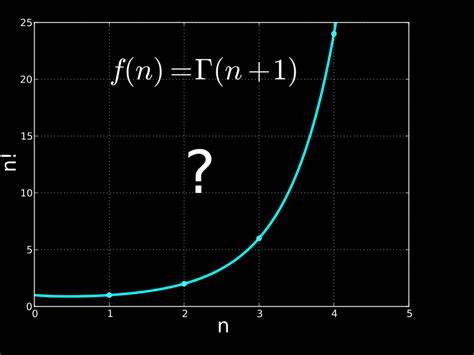
Podemos obtener ${displaystyle Gamma (1)}$:

Teniendo que ${displaystyle Gamma (1)=1=0!}$ y ${displaystyle Gamma (n+1)=nGamma (n)}$ entonces

para todos los naturales ${displaystyle n}$.

La función gamma es una función meromorfa de ${displaystyle zin mathbb {C} }$ con polos simples en ${displaystyle z=-n,,(n=0,,1,,2,,3,,dots )}$ y residuos ${displaystyle operatorname {Res} (Gamma (z),-n)={frac {(-1)^{n}}{n!}}}$.^[1]​ Estas propiedades pueden ser usadas para extender ${displaystyle Gamma (z)}$ desde su definición inicial a todo el plano complejo (exceptuando los puntos en los cuales es singular) por continuación analítica.

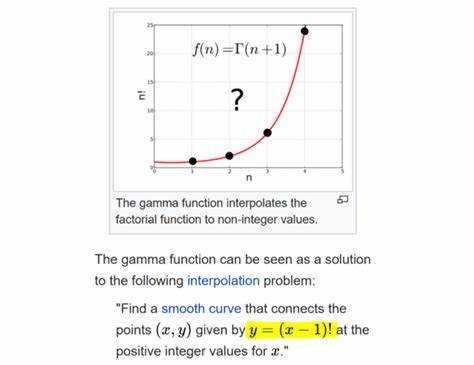
Para todo entero ${displaystyle m}$ se verifica

Si ${displaystyle m}$ no es un entero entonces no es posible decir si la ecuación anterior es válida pues en esta sección aún no se ha definido la función factorial para no enteros. Sin embargo, podemos obtener una extensión de la función factorial para no enteros exigiendo que esta relación siga siendo válida para un número complejo arbitrario ${displaystyle z}$:

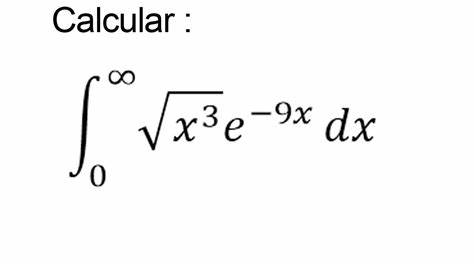
Al multiplicar ambos lados por ${displaystyle z!}$ se obtiene

Este producto infinito converge para todos los números complejos ${displaystyle z}$ excepto para enteros negativos en los que falla, ya que la relación recursiva ${displaystyle m!=m(m-1)!}$ hacia atrás lleva a una división entre cero para el valor ${displaystyle m=0}$. Puesto que ${displaystyle Gamma (n)=(n-1)!}$, para la función gamma la relación precedente da lugar a la definición:

válida para enteros no negativos.

La definición de la función gamma debida a Weierstrass es válida para todos los números complejos ${displaystyle z}$ excepto para valores enteros no positivos

donde ${displaystyle gamma }$ es la constante de Euler-Mascheroni.

Una representación de la función gamma incompleta en términos de los polinomios generalizados de Laguerre es

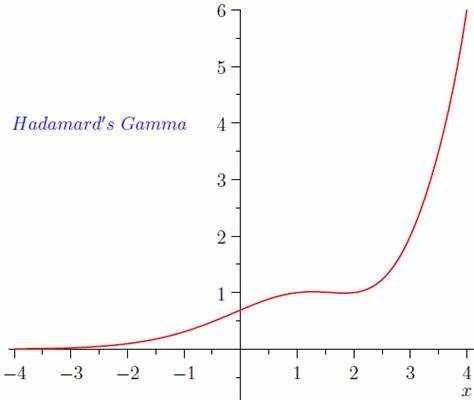
que converge para ${displaystyle { ext{Re}}(z)>-1}$ y ${displaystyle x>0}$.

Otras ecuaciones funcionales importantes de la función gamma son la fórmula de reflexión de Euler

que implica

y la fórmula de duplicación de Legendre

La fórmula de duplicación es un caso especial del teorema de multiplicación

Una propiedad básica pero muy útil de la función gamma, que puede obtenerse a partir de la definición en términos de un límite es

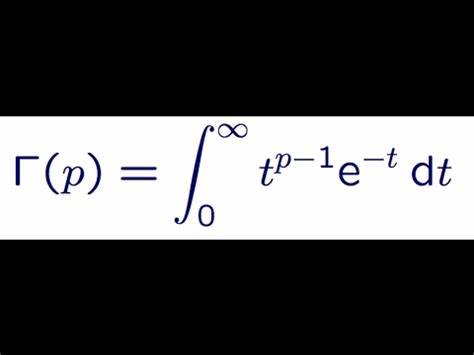
en particular, con ${displaystyle z=a+bi}$, este producto es

si la parte real es un entero, esto es ${displaystyle ain mathbb {Z} }$ entonces

siendo ${displaystyle nin mathbb {N} }$.

Varios límites útiles para aproximaciones asintóticas:

Quizá el valor más conocido de la función gamma con argumento no entero es:

La cual puede obtenerse haciendo ${displaystyle z=1/2}$ en la fórmula de reflexión o en la fórmula de duplicación, usando la relación de la función gamma con la función beta dada más abajo con ${displaystyle x=y=1/2}$ o haciendo la sustitución ${displaystyle u={sqrt {t}}}$ en la definición integral de la función gamma, con lo que se obtiene una integral Gaussiana. En general, para valores no negativos de ${displaystyle n}$ se tiene:

donde ${displaystyle n!!}$ denota al doble factorial de ${displaystyle n}$.

Las derivadas de la función gamma vienen dadas por la función poligamma, por ejemplo:

Para un entero positivo ${displaystyle m}$, la derivada de la función gamma puede calcularse como sigue

donde ${displaystyle gamma }$ denota la constante de Euler-Mascheroni.

A partir de la representación integral de la función gamma, se obtiene que la ${displaystyle n}$-ésima derivada de la función gamma viene dada por:

La función gamma tiene un polo de orden 1 en ${displaystyle z=-n}$ para todo número entero no negativo. El residuo en cada polo es:

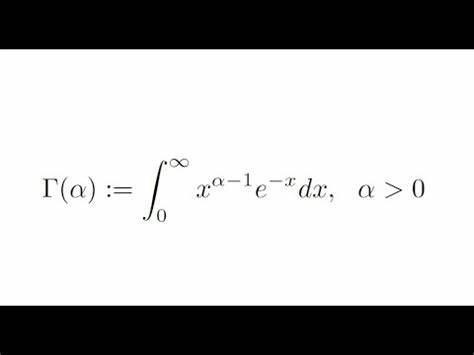
El teorema de Bohr-Mollerup dice que, entre todas las funciones que generalizan el factorial de los números naturales a los reales, solo la función gamma es logarítmicamente convexa, esto es, el logaritmo natural de la función gamma es una función convexa.

Hay muchas fórmulas, además de la integral de Euler de segundo tipo, para representa la función gamma como una integral. Cuando la parte real de ${displaystyle z}$ es positiva entonces

Cuando la parte real de ${displaystyle z}$ es positiva entonces la primera fórmula integral de Binet para la función gamma es

la integral de la derecha puede ser interpretada como la Transformada de Laplace, esto es

Cuando la parte real de ${displaystyle z}$ es positiva entonces la segunda fórmula integral de Binet para la función gamma es

El logaritmo de la función gamma tiene el siguiente desarrollo en series de Fourier para ${displaystyle 0<z<1}$:

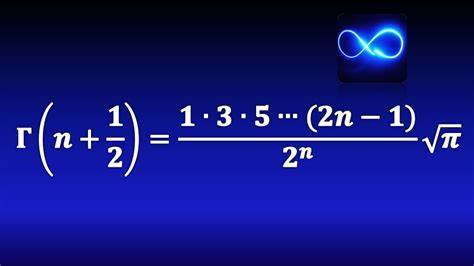
que por un largo tiempo se le atribuyó a Ernst Kummer quien lo demostró en 1847. Sin embargo, se descubrió que Carl Johan Malmsten la demostró por primera vez en 1842.

En 1840, Joseph Ludwig Raabe demostró que

para valores ${displaystyle a>0}$.

En particular, cuando ${displaystyle a=0}$ obtenemos

Gauss introdujo una notación alternativa de la función gamma denominada función Pi, que en términos de la función gamma es:

Así, la relación de la función Pi con el factorial es más natural que en el caso de la función gamma pues para cualquier entero no negativo ${displaystyle n}$

La fórmula de la reflexión toma la siguiente forma:

Donde ${displaystyle { ext{sinc}}}$ es la función sinc normalizada, mientras que el teorema de la multiplicación toma la forma:

En ocasiones se encuentra la siguiente definición

donde ${displaystyle pi (z)}$ es una función entera definida para todo número complejo, pues no tiene polos. La razón de ello es que la función gamma y, por tanto, la función Pi, no tienen ceros.

Fórmula válida solo si ${displaystyle operatorname {Re} (z)>1}$. También aparece en la ecuación funcional de ${displaystyle zeta (z)}$:

Algunos valores particulares de la función gamma son

La función gamma se puede calcular numéricamente con precisión arbitraria usando la fórmula de Stirling, la aproximación de Lanczos o la aproximación de Spouge.

Para argumentos que sean múltiplos enteros de 1/24, la función gamma puede ser evaluada rápidamente usando iteraciones de medias aritmético geométricas (véase Valores de la función gamma).

Debido a que tanto la función gamma como el factorial crecen muy rápidamente para argumentos moderadamente grandes, muchos programas de computación incluyen funciones que devuelven el logaritmo de la función gamma. Este crece más lentamente, y en cálculos combinatorios es muy útil, pues se pasa de multiplicar y dividir grandes valores a sumar o restar sus logaritmos.

La ${displaystyle n}$-ésima derivada de ${displaystyle ax^{b}}$ (donde n es un número natural) se puede ver de la siguiente manera:

como ${displaystyle n!=Gamma (n+1)}$ entonces

donde ${displaystyle n}$ puede ser cualquier número donde gamma esté definido o se pueda definir mediante límites. De esta manera se puede calcular por ejemplo, la 1/2 derivada de ${displaystyle x}$, de ${displaystyle x^{2}}$ e inclusive de una constante ${displaystyle c=cx^{0}}$:

---