Cuadrilátero

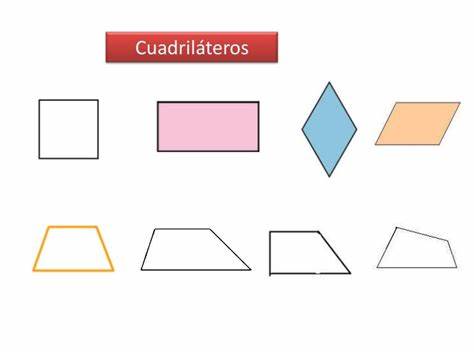
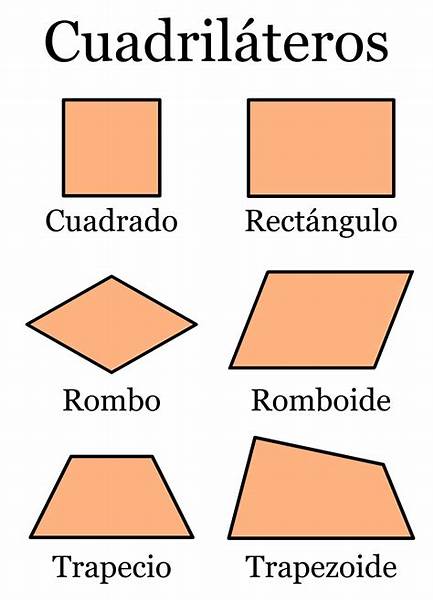
En geometría del plano euclídeo, un cuadrilátero es un polígono con cuatro aristas y cuatro vértices (o de forma coloquial, con cuatro lados y cuatro esquinas). A veces se usa el término cuadrángulo por analogía con triángulo, al igual que tetrágono por consistencia con pentágono (5 lados), hexágono (6 lados), y en general, con los polígonos de n lados (en este caso, con n=4 lados).

La palabra cuadrilátero se deriva de las palabras latinas "quadri", una variante de cuatro, y "latus", que significa "lado"

Los cuadriláteros son polígonos simples (no autointersecantes) o complejos (autointersecantes), también llamados cruzados. Los cuadriláteros simples también pueden clasificarse como convexos o cóncavos.

Los ángulos interiores de un cuadrilátero simple (y plano) ABCD, suman 360 grados, es decir

Es un caso especial de la fórmula de la suma de los ángulos interiores un n-gono, cuyo valor es (n-2)×180°.

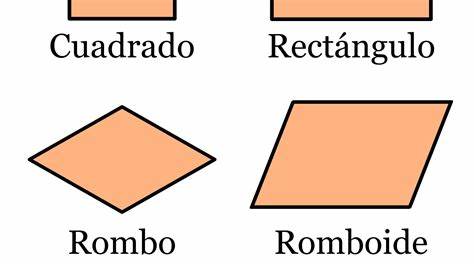
Todos los cuadriláteros cuyos lados no se cruzan entre sí, automáticamente recubren el plano mediante la rotación repetida alrededor de los puntos medios de sus lados.

Los elementos de un cuadrilátero son los siguientes:

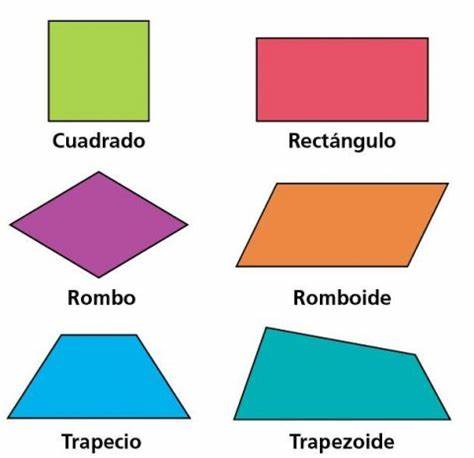
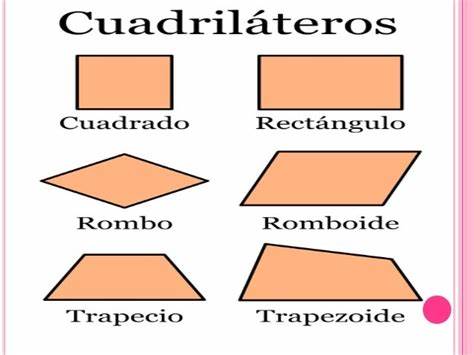
Los cuadriláteros se clasifican según el paralelismo de sus lados, sus longitudes y sus ángulos interiores:

En el gráfico ilustrativo de la taxonomía de los cuadriláteros se pasa de las definiciones más generales a las más específicas siguiendo el sentido de las flechas.

Así se parte de un cuadrilátero definido como un polígono cerrado de cuatro lados, sin más restricciones, para diferenciar a continuación los cuadriláteros compuestos de los simples.

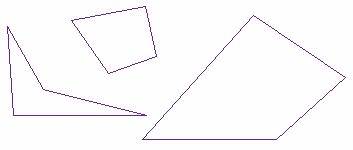
En un cuadrilátero complejo, dos de sus lados se cortan. En uno simple los lados no se cruzan.

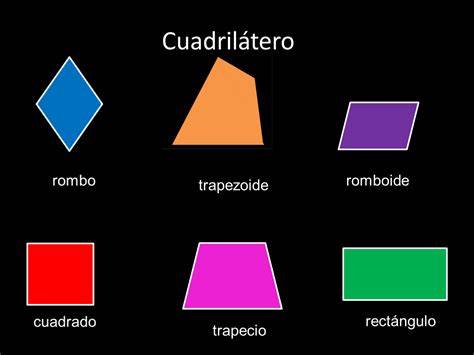
Los cuadriláteros simples se dividen en:

A un cuadrilátero que al mismo tiempo sea cíclico y tangencial se le denomina cuadrilátero bicéntrico. El deltoide es tangencial con dos pares de lados iguales.

Un caso particular de trapecio isósceles es cuando la longitud de una de las bases es igual que la de sus lados, por lo cual se configura un trapecio de tres lados iguales.

Cualquier cuadrilátero que no se autointerseca es un cuadrilátero simple.

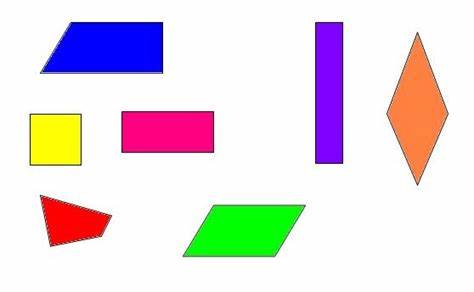
En un cuadrilátero convexo, todos los ángulos interiores son inferiores a 180° y las dos diagonales se encuentran dentro del cuadrilátero. Trapezoide o cuadrilátero irregular: ninguno de sus lados son paralelos entre sí

 

En un cuadrilátero cóncavo, un ángulo interior es mayor de 180° y una de las dos diagonales se encuentra fuera del cuadrilátero.

Un cuadrilátero autointersecante se puede denominar de varias formas: cuadrilátero cruzado, cuadrilátero mariposa o lazo de pajarita. En un cuadrilátero cruzado, los cuatro ángulos interiores a cada lado del cruce (dos agudos y dos obtusos, todos a la izquierda o todos a la derecha a medida que se traza la figura) suman 720°.^[10]​

Los cuadriláteros también pueden clasificarse de acuerdo con sus propiedades de simetría:

Ejes de simetría:

Simetría rotacional:

Estos criterios también son aplicables a los cuadriláteros complejos:

Ejes de simetría:

Simetría rotacional:

El resto de los cuadriláteros carece de simetrías.

${displaystyle A={ frac {1}{2}}adcdot sin {alpha }+{ frac {1}{4}}{sqrt {4b^{2}c^{2}-(b^{2}+c^{2}-a^{2}-d^{2}+2adcdot cos {alpha })^{2}}}}$ (para un cuadrilátero con concavidad en C cambiar el primer signo + por -).

Sea el cuadrilátero inscrito de lados a,b,c y d; de diagonales perpendiculares que al intersecarse determinan los segmentos m y n en uno de ellos, y p y q en el otro, y cuyo radio de la circunferencia circunscrita se denomina R. En tal caso, son válidas las igualdades siguientes:^[12]​

${displaystyle a^{2}+c^{2}=b^{2}+d^{2}=4R^{2}}$

(1)${displaystyle m^{2}+n^{2}+p^{2}+q^{2}=4R^{2}}$

Las dos diagonales de un cuadrilátero convexo son los segmentos que conectan vértices opuestos.

Las dos bimedianas de un cuadrilátero convexo son los segmentos rectilíneos que conectan los puntos medios de los lados opuestos.^[13]​ Se cruzan en el centroide de vértices del cuadrilátero.

Las cuatro m-alturas de un cuadrilátero convexo son las perpendiculares a un lado a través del punto medio del lado opuesto. ^[14]​

Existen varias fórmulas generales para el área K de un cuadrilátero convexo ABCD con lados a = AB, b = BC, c = CD y d = DA.

El área se puede expresar en términos trigonométricos como

donde las longitudes de las diagonales son p y q y el ángulo entre ellas es θ. ^[15]​ En el caso de un cuadrilátero ortodiagonal (por ejemplo, rombo, cuadrado o deltoide), esta fórmula se reduce a ${displaystyle K={ frac {1}{2}}pq}$ ya que θ es 90°.

El área también se puede expresar en términos de las bimedianas como^[16]​

donde las longitudes de las bimedianas son m y n y el ángulo entre ellos es φ.

La fórmula de Bretschneider^[17]​ expresa el área en términos de la longitud de los lados y del valor de dos ángulos opuestos:

donde los lados (denominados consecutivamente) son a, b, c y d, donde s es el semiperímetro, y donde A y C son dos (de hecho, cualesquiera dos) ángulos opuestos. Esto se reduce a la fórmula de Brahmagupta para el área de un cuadrilátero cíclico cuando A + C = 180°.

Otra fórmula del área en función de la longitud de los lados y del valor de los ángulos, con el ángulo C entre los lados b y c, y A entre los lados a y d, es

En el caso de un cuadrilátero cíclico, la última fórmula se convierte en ${displaystyle K={ frac {1}{2}}(ad+bc)sin {A}.}$

En un paralelogramo, donde ambos pares de lados opuestos y ángulos son iguales, esta fórmula se reduce a ${displaystyle K=abcdot sin {A}.}$

Alternativamente, se puede determinar el área en términos de los lados y el ángulo de intersección θ de las diagonales, siempre que este ángulo no sea 90°:^[18]​

En el caso de un paralelogramo, la última fórmula se convierte en ${displaystyle K={ frac {1}{2}}| an heta |cdot left|a^{2}-b^{2} ight|.}$

Otra fórmula del área que incluye los lados a, b, c y d, es:^[16]​

donde x es la distancia entre los puntos medios de las diagonales y φ es el ángulo entre las bimedianas.

La última fórmula del área trigonométrica que incluye los lados a, b, c y d y el ángulo α entre a y b, es:^{[cita requerida]}

que también se puede usar para el área de un cuadrilátero cóncavo (que tiene la parte cóncava opuesta al ángulo α) simplemente cambiando el primer signo + por un -.

Las siguientes dos fórmulas expresan el área en términos de los lados a, b, c y d; del semiperímetro s y de las diagonales p y q:

La primera se reduce a la fórmula de Brahmagupta en el caso del cuadrilátero cíclico, dado que entonces pq = ac + bd.

El área también se puede expresar en términos de las bimedianas m y n; y de las diagonales p y q:

De hecho, tres de los cuatro valores m, n, p y q son suficientes para la determinación del área, ya que en cualquier cuadrilátero los cuatro valores están relacionados por ${displaystyle p^{2}+q^{2}=2(m^{2}+n^{2}).}$^[23]​^{: p. 126} Las expresiones correspondientes son:^[24]​

si se dan las longitudes de dos bimedianas y de una diagonal, y^[24]​

si se dan las longitudes de dos diagonales y de una bimediana.

El área de un cuadrilátero ABCD se puede calcular usando vectores. Sean los vectores AC y BD correspondientes a las diagonales desde A hasta C y desde B hasta D. El área del cuadrilátero es entonces

que es la mitad de la magnitud del producto vectorial de los vectores AC y BD. En el espacio euclidiano bidimensional, expresando el vector AC como un vector libre en el espacio cartesiano igual a (x₁, y₁) y BD como (x₂, y₂), esto puede reescribirse como:

En la siguiente tabla se enumera si las diagonales en algunos de los cuadriláteros más básicos se bisecan entre sí, si sus diagonales son perpendiculares y si sus diagonales tienen la misma longitud.^[25]​ La lista se aplica a los casos más generales:

Nota 1: Los trapecios (incluidos los trapecios isósceles), en general no tienen diagonales perpendiculares, pero hay un número infinito de trapecios (no semejantes entre sí) y de trapecios isósceles, que tienen diagonales perpendiculares y no son ningún otro tipo de cuadrilátero.

Nota 2: En un deltoide, una diagonal divide a la otra. El deltoide más general tiene diagonales desiguales, pero hay un número infinito de deltoides (no similares) en los que las diagonales tienen la misma longitud (y que no se ajustan a la definición de otro cuadrilátero).

Las longitudes de las diagonales en un cuadrilátero convexo ABCD se pueden calcular usando el teorema del coseno en cada triángulo formado por una diagonal y dos lados del cuadrilátero. Así

y

Otras fórmulas más simétricas para las longitudes de las diagonales son:^[26]​

y

En cualquier cuadrilátero convexo ABCD, la suma de los cuadrados de los cuatro lados es igual a la suma de los cuadrados de las dos diagonales más cuatro veces el cuadrado de la longitud del segmento que conecta los puntos medios de las diagonales. Así

donde x es la distancia entre los puntos medios de las diagonales.^[23]​^: p.126 Esto a veces se conoce como el teorema del cuadrilátero de Euler y es una generalización de la ley del paralelogramo.

El matemático alemán Carl Anton Bretschneider dedujo en 1842 la siguiente generalización del Teorema de Ptolomeo con respecto al producto de las diagonales en un cuadrilátero convexo:^[27]​

Esta relación puede considerarse como equivalente al teorema del coseno para un cuadrilátero. En un cuadrilátero cíclico, donde A+C=180°, se reduce a pq=ac+bd. Como cos(A+C)≥−1, también proporciona una prueba de la desigualdad de Ptolomeo.

Si X e Y son los pies de las normales desde B y D hasta la diagonal AC=p en un cuadrilátero convexo ABCD con lados a=AB, b=BC, c=CD y d=DA, entonces^[28]​^: p.14

En un cuadrilátero convexo ABCD con lados a=AB, b=BC, c=CD y d=DA, y donde las diagonales se cruzan en E,

donde e=AE, f=BE, g=CE, y h=DE.^[29]​

La forma y el tamaño de un cuadrilátero convexo están completamente determinados por las longitudes de sus lados en secuencia y de una diagonal entre dos vértices especificados. Las dos diagonales p, q y las cuatro longitudes laterales a, b, c, d de un cuadrilátero están relacionadas^[30]​ por el determinante de Cayley-Menger, de la siguiente manera:

Las bisectrices internas de un cuadrilátero convexo forman un cuadrilátero cíclico^[23]​^: p.127 (es decir, los cuatro puntos de intersección de las bisectrices adyacentes son cocíclicos) o son concurrentes. En el último caso, se trata de un cuadrilátero circunscrito.

En el cuadrilátero ABCD, si las bisectrices de A y C coinciden con la diagonal BD, entonces las bisectrices de B y D se encuentran sobre la diagonal AC.^[31]​

Las bimedianas de un cuadrilátero son los segmentos de línea que conectan los puntos medios de los lados opuestos. La intersección de las bimedianas es el centroide de los vértices del cuadrilátero. ^[32]​

Los puntos medios de los lados de cualquier cuadrilátero (convexo, cóncavo o cruzado) son los vértices de un paralelogramo, llamado paralelogramo de Varignon. Tiene las siguientes propiedades:

Las dos bimedianas de un cuadrilátero y el segmento que une los puntos medios de las diagonales de ese cuadrilátero son concurrentes, y todas quedan divididas en dos partes iguales por su punto de intersección.^[23]​^: p.125

En un cuadrilátero convexo con lados a, b, c y d, la longitud de la bimediana que conecta los puntos medios de los lados a y c es

donde p y q son las longituded de las diagonales.^[34]​ La longitud de la bimediana que conecta los puntos medios de los lados b y d es

Por lo tanto,^[23]​^: p.126

Este también es un corolario a la ley del paralelogramo aplicada sobre el paralelogramo de Varignon.

Las longitudes de las bimedianas también se pueden expresar en términos de dos lados opuestos y la distancia x entre los puntos medios de las diagonales. Esto es posible cuando se usa el teorema del cuadrilátero de Euler en las fórmulas anteriores. Entonces^[22]​

y

Téngase en cuenta que los dos lados opuestos en estas fórmulas son los dos que no conecta la bimediana.

En un cuadrilátero convexo, existe la siguiente conexión dual entre las bimedianas y las diagonales:^[28]​

Los cuatro ángulos de un cuadrilátero simple ABCD satisfacen las siguientes identidades: ^[35]​

y

Además, ^[36]​

En las últimas dos fórmulas, no se permite que ningún ángulo sea un ángulo recto, dado que tan 90° (la función trigonométrica tangente de un ángulo recto), no está definida.

Si un cuadrilátero convexo tiene los lados consecutivos a, b, c y d; y las diagonales p y q; entonces su área K satisface^[37]​

De la fórmula de Bretschneider se deduce directamente que el área de un cuadrilátero satisface que

dándose la igualdad si y solo si el cuadrilátero es cíclico o degenerado, de tal manera que la longitud de un lado es igual a la suma de los otros tres (es decir, ha colapsado en un segmento, por lo que su área es cero).

El área de cualquier cuadrilátero también satisface la desigualdad^[38]​

Denotando el perímetro como L, se tiene que^[38]​^: p.114

con igualdad solo en el caso de un cuadrado.

El área de un cuadrilátero convexo también satisface que

para longitudes de las diagonales p y q, verificándose la igualdad si y solo si las diagonales son perpendiculares.

Sean a, b, c y d las longitudes de los lados de un cuadrilátero convexo ABCD con el área K y diagonales AC=p y BD=q. Entonces^[39]​

Sean a, b, c y d las longitudes de los lados de un cuadrilátero convexo ABCD con el área K. Entonces, se cumple la siguiente desigualdad:^[40]​

Un corolario del teorema del cuadrilátero de Euler es la desigualdad

donde la igualdad se cumple si y solo si el cuadrilátero es un paralelogramo.

Euler también generalizó el teorema de Ptolomeo, que es una igualdad para un cuadrilátero cíclico, en una desigualdad para un cuadrilátero convexo. Afirma que

donde se verifica la igualdad sí y solo si el cuadrilátero es cíclico.^[23]​^{: p.128–129} Esta relación a menudo se denomina desigualdad de Ptolomeo.

En cualquier cuadrilátero convexo, las bimedianas m y n, y las diagonales p y q están relacionadas por la desigualdad

verificándose la igualdad si y solo si las diagonales son iguales.^[41]​^: Prop.1 Esto se deduce directamente de la identidad del cuadrilátero

Los lados a, b, c y d de cualquier cuadrilátero satisfacen que ^[42]​^{: p.228, #275}

y además^[42]​^{: p.234, #466}

Entre todos los cuadriláteros con un perímetro dado, el que tiene el área más grande es el cuadrado. Esto se llama teorema isoperimétrico para cuadriláteros. Es una consecuencia directa de la desigualdad del área^[38]​ ^: p.114

donde K es el área de un cuadrilátero convexo con perímetro L. La igualdad se cumple sí y solo si el cuadrilátero es un cuadrado. El doble teorema establece que de todos los cuadriláteros con un área dada, el cuadrado tiene el perímetro más corto. El cuadrilátero con longitudes laterales dadas que tiene el área máxima es el cuadrilátero cíclico.^[43]​ De todos los cuadriláteros convexos con diagonales dadas, el cuadrilátero ortodiagonal tiene el área más grande.^[38]​ ^: p.119 Esto es una consecuencia directa del hecho de que el área de un cuadrilátero convexo satisface la condición

donde θ es el ángulo entre las diagonales p y q. La igualdad se cumple si y solo si θ=90°. Si P es un punto interior en un cuadrilátero convexo ABCD, entonces

De esta desigualdad se deduce que el punto dentro de un cuadrilátero que minimiza la suma de distancias a los vértices es la intersección de las diagonales. Por lo tanto, ese punto es el punto de Fermat de un cuadrilátero convexo.^[44]​ ^: p.120

El centro de un cuadrilátero se puede definir de varias maneras diferentes. El "centroide de vértices" proviene de considerar el cuadrilátero como vacío pero con masas iguales en sus vértices. El "centroide lateral" viene de considerar que los lados tienen masa constante por unidad de longitud. El centro habitual, llamado simplemente centroide (centro del área), proviene de considerar que la superficie del cuadrilátero tiene una densidad constante. En general, estos tres puntos no son todos el mismo punto.^[45]​ El "centroide de vértices" es la intersección de las dos bimedianas.^[46]​ Como con cualquier polígono, las coordenadas x e y del centroide de vértices son las medias aritméticas de las coordenadas x e y de los vértices. El "centroide del área" del cuadrilátero ABCD se puede construir de la siguiente manera. Sean G_a, G_b, G_c, G_d los centroides de los triángulos BCD, ACD, ABD, ABC respectivamente. Entonces, el "centroide del área" es la intersección de las rectas G_aG_c y G_bG_d.^[47]​

En un cuadrilátero convexo general ABCD, no existen analogías naturales con la circunferencia circunscrita y la altura de un triángulo. Pero dos de estos puntos se pueden construir de la siguiente manera. Sean O_a, O_b, O_c, O_d los circuncentros de los triángulos BCD, ACD, ABD, ABC respectivamente; y sean H_a, H_b, H_c y H_d los ortocentros de los mismos triángulos. Entonces, la intersección de las líneas O_a O_c y O_b O_d se denomina cuasicircuncentro, y la intersección de las líneas H_aH_c y H _bH_d se llama el cuasiortocentro del cuadrilátero convexo.^[47]​ Estos puntos se pueden usar para definir una recta de Euler de un cuadrilátero. En un cuadrilátero convexo, el cuasiortocentro H, el "centroide de área" G y el cuasicircuncentro O son colineales en este orden, y HG=2GO.^[47]​ También se puede definir un cuasicentro de nueve puntos E como la intersección de las líneas E_aE_c y E_bE_d, donde E_a, E_b, E_c, E_d son los centros de los nueve puntos de los triángulos BCD, ACD, ABD, y ABC respectivamente. Entonces E es el punto medio de OH.^[47]​ Otra línea notable en un cuadrilátero convexo no paralelogramo es la línea de Newton, que conecta los puntos medios de las diagonales, el segmento que conecta estos puntos pasa por el centroide de los vértices. Una línea más interesante (en cierto sentido dual a la línea de Newton) es la recta que conecta el punto de intersección de las diagonales con el centroide de los vértices. La línea es notable por el hecho de que contiene el centroide (área). El centroide de los vértices divide el segmento que conecta la intersección de las diagonales y el centroide (área) en la proporción 3:1.^[48]​

Para cualquier cuadrilátero ABCD con puntos P y Q, construidos como las intersecciones de AD y BC y de AB y CD, respectivamente, los círculos (PAB), (PCD), (QAD), y (QBC) pasan a través de un punto común M, llamado punto de Miquel.^[49]​

Un cuadrilátero no plano se llama "cuadrilátero alabeado". Las fórmulas para calcular sus ángulos diédricos a partir de las longitudes de los lados y el ángulo entre dos lados adyacentes se utilizan para trabajar en las propiedades de moléculas como el ciclobutano, que contienen un anillo "alabeado" de cuatro átomos.^[51]​ Históricamente, el término cuadrilátero gauche (término tomado del francés, con el significado de no plano) también se usó para referirse a un cuadrilátero alabeado.^[52]​ Un cuadrilátero alabeado junto con sus diagonales forma un tetraedro (posiblemente no regular), y por el contrario, cada cuadrilátero alabeado proviene de un tetraedro al que se le eliminan un par de aristas opuestas.

---